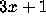The ideas behind Terras's analysis seem basic to a deeper understanding
of the 
problem, so I describe them in detail.
In order to do this, I introduce some notation to
describe the results of the process of iterating the function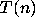 
.
Given an integer n, define a sequence of 0-1 valued
quantities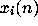 
by
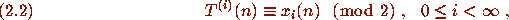where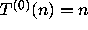 
.
The results of first k iterations of T are completely described by the
parity vector
since the result of k iterations is
where
and
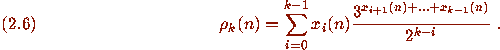Note that in (2.5), (2.6) both 
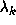and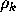 
are completely determined by the parity vector 
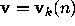given by
(2.3); I sometimes indicate this by writing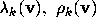 
(instead of 
.
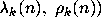The formula (2.4) shows that a necessary condition for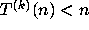 
is that
since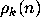 
is nonnegative.
Terras [67] defines the coefficient stopping time
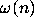to be the least value of k such that (2.7) holds,
and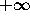 
if no such value of k exists.
It is immediate that
The function 
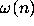plays an important role in the analysis of the
behavior of the stopping time function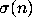 
, see Theorem C.