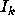 with a given coefficient
stopping time k is a set of arithmetic progressions
with a given coefficient
stopping time k is a set of arithmetic progressions
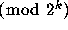 , which has the immediate consequence that
, which has the immediate consequence that 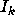 has the
asymptotic density
has the
asymptotic density

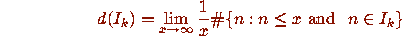 which is given by
which is given by

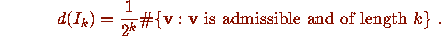 Furthermore Theorem C asserts that the set
Furthermore Theorem C asserts that the set

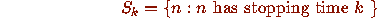 differs from
differs from 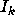 by a finite set, so that
by a finite set, so that 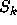 also has an asymptotic density
which is the same as that of
also has an asymptotic density
which is the same as that of 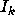 .
Consequently, Theorem C implies the first part of Theorem A, that the set
of all integers with stopping time at most k have an asymptotic density
.
Consequently, Theorem C implies the first part of Theorem A, that the set
of all integers with stopping time at most k have an asymptotic density 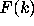 given by
given by

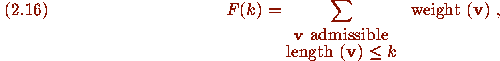 where
where

 Now the formula (2.16) can be used to prove the second part of Theorem A,
and in fact to prove the stronger result that
Now the formula (2.16) can be used to prove the second part of Theorem A,
and in fact to prove the stronger result that 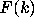 approaches 1 at an exponential rate as
approaches 1 at an exponential rate as 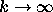 .
.