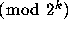 , as described
by part (i) of Theorem C.
Furthermore, the truth of the Coefficient Stopping Time Conjecture implies
that there are no nontrivial cycles.
To see this, suppose that there were a
nontrivial cycle of period k and let
, as described
by part (i) of Theorem C.
Furthermore, the truth of the Coefficient Stopping Time Conjecture implies
that there are no nontrivial cycles.
To see this, suppose that there were a
nontrivial cycle of period k and let 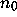 be its smallest element,
and note that
be its smallest element,
and note that 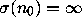 .
Then
.
Then 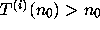 for
for 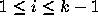 and
and

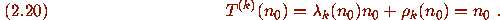 Now
Now 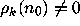 since
since 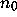 isn't a
power of 2, so that (2.20) implies that
isn't a
power of 2, so that (2.20) implies that 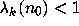 .
Hence
.
Hence 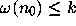 , so that
, so that
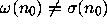 .
.