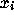 are fixed.
In fact, considerably more can be proved about the nonexistence of nontrivial
cyclic trajectories using special features of the necessary condition
(2.24).
For example, several authors have independently found a much more efficient
computational procedure for proving the nonexistence of nontrivial
cyclic trajectories of period
are fixed.
In fact, considerably more can be proved about the nonexistence of nontrivial
cyclic trajectories using special features of the necessary condition
(2.24).
For example, several authors have independently found a much more efficient
computational procedure for proving the nonexistence of nontrivial
cyclic trajectories of period 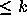 ; it essentially makes use of the
inequality
; it essentially makes use of the
inequality

 which must hold for
which must hold for 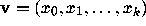 satisfying (2.24).
This approach also allows one to check the truth of the
Coefficient Stopping Time Conjecture for all n with
satisfying (2.24).
This approach also allows one to check the truth of the
Coefficient Stopping Time Conjecture for all n with
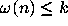 .
The basic result is as follows.
.
The basic result is as follows.