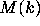Theorem H can be used to show the nonexistence of nontrivial cycles of small period by obtaining upper bounds for the

and checking that condition (i) holds. This approach has been taken by Crandall [28], Garner [34], Schuppar [61] and Terras [67]. In estimating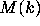

, one can show that the quantities

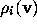are never very large, so that the size of

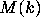is essentially determined by how large

can get. The worst cases occur when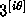

is a very close approximation to

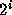, i.e., when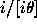

is a very good rational approximation to

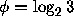. The best rational approximations to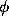

are given by the convergents

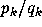of the continued fraction expansion of

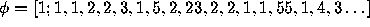. Crandall [28] uses general properties of continued fraction convergents to obtain the following quantitative result.

Annotation Form Interface
Your name: E-Mail address: Annotation Subject: Related URL: