Further information about the nonexistence of nontrivial cyclic trajectories can be obtained by treating the necessary condition (2.24) as an nonexponential Diophantine equation. Davidson [29] calls a purely periodic trajectory of period k a circuit if there is a value i for which

and

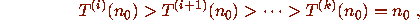i.e., the parity vector 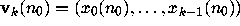has the special form

 

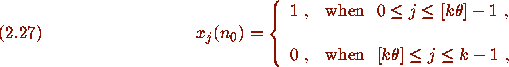where 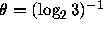. The cycle starting with 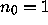is a circuit. Davidson observed that each solution to the exponential Diophantine equation

 

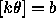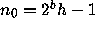gives rise to a circuit of length k = a + b with and , and conversely. (The equation (2.28) is the necessary condition (2.24) specialized to the vector (2.27). R. Steiner [64] showed that 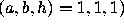is the only solution of (2.28), thus proving the following result.