
 and
and

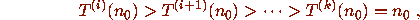 i.e., the parity vector
i.e., the parity vector 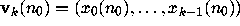 has the special form
has the special form

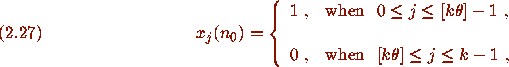 where
where 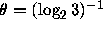 .
The cycle starting with
.
The cycle starting with 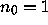 is a circuit.
Davidson observed that each solution to the exponential
Diophantine equation
is a circuit.
Davidson observed that each solution to the exponential
Diophantine equation

 gives rise to a circuit of length k = a + b with
gives rise to a circuit of length k = a + b with 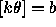 and
and 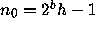 , and conversely.
(The equation (2.28) is the necessary condition (2.24) specialized
to the vector (2.27).
R. Steiner [64] showed that
, and conversely.
(The equation (2.28) is the necessary condition (2.24) specialized
to the vector (2.27).
R. Steiner [64] showed that 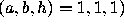 is the only solution of (2.28), thus proving the following result.
is the only solution of (2.28), thus proving the following result.