![[Shownotes]](../gif/annotate/shide-21.gif)
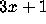 problem are most elegantly expressed in
terms of iterations of the function
problem are most elegantly expressed in
terms of iterations of the function

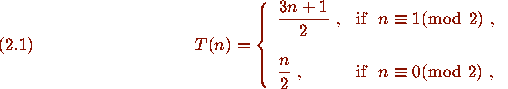 One way to think of the
One way to think of the 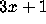 problem involves a directed graph whose
vertices are the positive integers and that has directed edges from n
to
problem involves a directed graph whose
vertices are the positive integers and that has directed edges from n
to 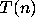 .
I call this graph the Collatz graph of
.
I call this graph the Collatz graph of 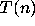 in honor of
L. Collatz [25].
A portion of the Collatz graph of
in honor of
L. Collatz [25].
A portion of the Collatz graph of 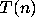 is pictured in Fig. 1.
A directed graph is said to be weakly connected
if it is connected when viewed as an undirected graph,
i.e., for any two vertices there is a path of edges joining them,
ignoring the directions on the edges.
The
is pictured in Fig. 1.
A directed graph is said to be weakly connected
if it is connected when viewed as an undirected graph,
i.e., for any two vertices there is a path of edges joining them,
ignoring the directions on the edges.
The 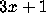 Conjecture can be formulated in terms of the
Collatz graph as follows.
Conjecture can be formulated in terms of the
Collatz graph as follows.
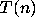 on the positive integers is weakly connected.
on the positive integers is weakly connected.
We call the sequence of iterates 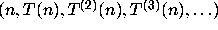 the trajectory of n.
There are three possible behaviors for such trajectories when n > 0.
the trajectory of n.
There are three possible behaviors for such trajectories when n > 0.
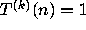 .
.
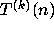 eventually becomes periodic and
eventually becomes periodic and 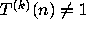 for any
for any 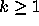 .
.
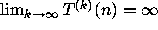 .
.
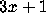 Conjecture asserts that all trajectories of positive n are
convergent.
It is certainly true for n > 1 that
Conjecture asserts that all trajectories of positive n are
convergent.
It is certainly true for n > 1 that
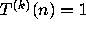 cannot occur without some
cannot occur without some 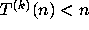 occurring.
Call the least
positive k for which
occurring.
Call the least
positive k for which 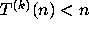 the
stopping time
the
stopping time
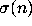 of n, and set
of n, and set 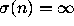 if no k occurs
with
if no k occurs
with 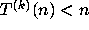 .
Also call the least positive k for which
.
Also call the least positive k for which 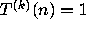 the total stopping time
the total stopping time
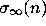 of n, and set
of n, and set 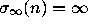 if no such k occurs.
We may restate the
if no such k occurs.
We may restate the 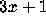 Conjecture in terms of the stopping time
as follows.
Conjecture in terms of the stopping time
as follows.
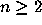 has a finite stopping time.
has a finite stopping time.
The appeal of the 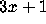 problem lies in the irregular behavior of the
successive iterates
problem lies in the irregular behavior of the
successive iterates 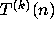 .
One can measure this behavior using the stopping time, the total stopping
time, and the
expansion factor
.
One can measure this behavior using the stopping time, the total stopping
time, and the
expansion factor
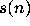 defined by
defined by

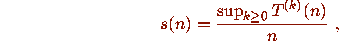 if n has a bounded trajectory and
if n has a bounded trajectory and 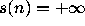 if n has a divergent
trajectory.
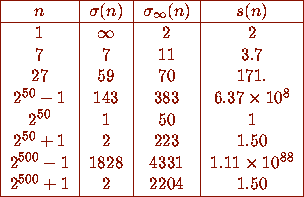
For example n = 27 requires 70 iterations to arrive at the value 1 and
if n has a divergent
trajectory.
For example n = 27 requires 70 iterations to arrive at the value 1 and

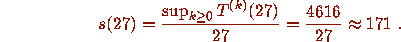 Table 1 illustrates the concepts defined so far by giving data on the
iterates
Table 1 illustrates the concepts defined so far by giving data on the
iterates  for selected values of n.
for selected values of n.
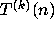 .
.

The 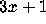 Conjecture has been numerically checked for a large range of
values of n.
It is an interesting problem to find efficient algorithms to test the
conjecture on a computer.
The current record for verifying the
Conjecture has been numerically checked for a large range of
values of n.
It is an interesting problem to find efficient algorithms to test the
conjecture on a computer.
The current record for verifying the 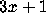 Conjecture seems to be held
by Nabuo Yoneda at the University of Tokyo,
who has reportedly checked it for all
Conjecture seems to be held
by Nabuo Yoneda at the University of Tokyo,
who has reportedly checked it for all 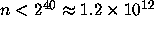 [2].
In several places the statement appears that A. S. Fraenkel has checked that
all
[2].
In several places the statement appears that A. S. Fraenkel has checked that
all 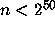 have a finite total stopping time;
this statement is erroneous [32].
have a finite total stopping time;
this statement is erroneous [32].