![[Shownotes]](../gif/annotate/shide-31.gif)
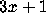 Conjecture (see [28]).
Pick an odd integer
Conjecture (see [28]).
Pick an odd integer 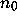 at random and iterate the function T
until another odd integer
at random and iterate the function T
until another odd integer 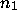 occurs.
Then
occurs.
Then 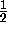 of the time
of the time 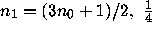 of the time
of the time 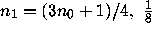 of the time
of the time 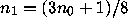 , and so on.
If one supposes that the function T is sufficiently ``mixing''
that successive odd integers in the trajectory of n
behave as though they were drawn at random
, and so on.
If one supposes that the function T is sufficiently ``mixing''
that successive odd integers in the trajectory of n
behave as though they were drawn at random
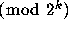 from the set of odd integers
from the set of odd integers
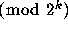 for all k, then the
expected growth in size between two consecutive odd integers in such a
trajectory is the multiplicative factor
for all k, then the
expected growth in size between two consecutive odd integers in such a
trajectory is the multiplicative factor

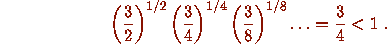 Consequently this heuristic argument suggests that on average the iterates in
a trajectory tend to shrink in size, so that divergent trajectories should not
exist.
Furthermore it suggests that the total stopping time
Consequently this heuristic argument suggests that on average the iterates in
a trajectory tend to shrink in size, so that divergent trajectories should not
exist.
Furthermore it suggests that the total stopping time
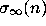 is (in some average sense) a constant multiple of
is (in some average sense) a constant multiple of 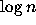 .
(Click here for more.)
.
(Click here for more.)
From the viewpoint of this heuristic argument, the central difficulty of the
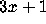 problem lies in understanding in detail the ``mixing'' properties of
iterates of the function
problem lies in understanding in detail the ``mixing'' properties of
iterates of the function 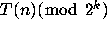 for all powers of 2.
The function
for all powers of 2.
The function 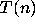 does indeed have some ``mixing'' properties given by
Theorems B and K below;
these are much weaker than what one needs to settle the
does indeed have some ``mixing'' properties given by
Theorems B and K below;
these are much weaker than what one needs to settle the 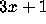 Conjecture.
Conjecture.