help annotate
Contents Next: Connections of the Up: The 3x+1 problem. Previous: Are there non-trivial

[Annotate][Shownotes]

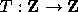Several authors have observed that heuristic probabilistic arguments suggest that no divergent trajectories occur.
DIVERGENT TRAJECTORIES CONJECTURE. The function has no divergent trajectories, i.e., there exists no integer 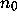for which

 

If a divergent trajectory 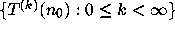exists, it cannot be equidistributed 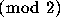. Indeed if one defines

then it can be proved that the condition (2.30) implies that

 

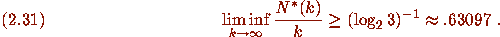
Theorem F constrains the possible behavior of divergent trajectories. Indeed, associated to any divergent trajectory 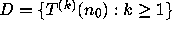is the infinite set 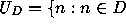and 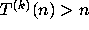for all 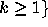. Since 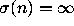for all 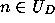, Theorem F implies that

 

where 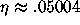. Roughly speaking, (2.32) asserts that the elements of a divergent trajectory cannot go to infinity ``too slowly.''
help annotate
Contents Next: Connections of the Up: The 3x+1 problem. Previous: Are there non-trivial