
Theorem C
(Terras).
(a)
The set of integers with coefficient stopping time k are exactly
the set of integers in those congruence classes  for which there is an admissible vector
for which there is an admissible vector 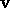 of length k with
of length k with 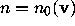 .
.
(b) Let 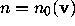 for some vector
for some vector 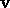 of length k.
If
of length k.
If 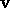 is admissible, then all sufficiently large integers congruent to
is admissible, then all sufficiently large integers congruent to
 have stopping time k.
If
have stopping time k.
If 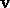 is not admissible, then only finitely many integers
congruent to
is not admissible, then only finitely many integers
congruent to  have stopping time k.
have stopping time k.
Proof C
The assertions made in (a) about coefficient stopping times follow from the
definition of admissibility, because that definition asserts that
(i) 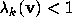 ,
,
(ii) 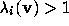 for
for 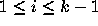 .
.
To prove (b), first note that if 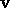 is admissible of length k, then
is admissible of length k, then

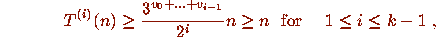 and so all elements of
and so all elements of 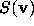 have stopping time at least k.
Now define
have stopping time at least k.
Now define 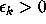 by
by

 where
where 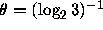 , and note that (2.11) implies that
, and note that (2.11) implies that

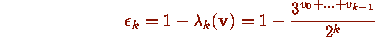 for all admissible
for all admissible 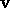 .
Now for
.
Now for 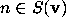 for an admissible
for an admissible 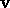 , (2.4) may be rewritten as
, (2.4) may be rewritten as

 Hence when
Hence when 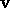 is admissible, those n in
is admissible, those n in 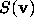 with
with

 have stopping time k, and
have stopping time k, and 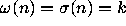 in this case.
in this case.
Now suppose 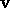 is not admissible.
There are two cases,
depending on whether or not some initial segment
is not admissible.
There are two cases,
depending on whether or not some initial segment
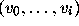 of
of 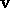 is admissible.
No initial segment of
is admissible.
No initial segment of 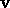 is admissible if and only if
is admissible if and only if

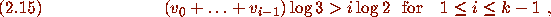 and when (2.15) holds say that
and when (2.15) holds say that 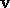 is inflating.
If
is inflating.
If 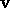 is inflating,
is inflating,
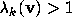 so that
so that 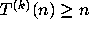 for all n in
for all n in 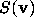 by (2.4),
so that no elements of
by (2.4),
so that no elements of 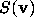 have stopping time k or less.
In the remaining case
have stopping time k or less.
In the remaining case 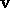 has an initial segment
has an initial segment 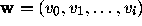 with i < k -1 which is admissible.
Now
with i < k -1 which is admissible.
Now 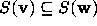 and all sufficiently large elements of
and all sufficiently large elements of
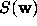 have stopping time i + 1 < k by the argument just given.
have stopping time i + 1 < k by the argument just given.

 for which there is an admissible vector
for which there is an admissible vector 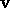 of length k with
of length k with 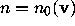 .
.
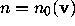 for some vector
for some vector 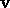 of length k.
If
of length k.
If 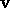 is admissible, then all sufficiently large integers congruent to
is admissible, then all sufficiently large integers congruent to
 have stopping time k.
If
have stopping time k.
If 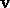 is not admissible, then only finitely many integers
congruent to
is not admissible, then only finitely many integers
congruent to  have stopping time k.
have stopping time k.
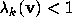
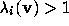
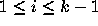
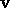

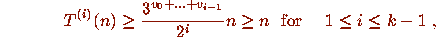 and so all elements of
and so all elements of 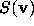 have stopping time at least k.
Now define
have stopping time at least k.
Now define 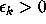 by
by

 where
where 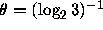 , and note that (2.11) implies that
, and note that (2.11) implies that

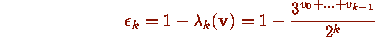 for all admissible
for all admissible 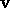 .
Now for
.
Now for 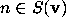 for an admissible
for an admissible 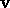 , (2.4) may be rewritten as
, (2.4) may be rewritten as

 Hence when
Hence when 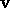 is admissible, those n in
is admissible, those n in 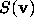 with
with

 have stopping time k, and
have stopping time k, and 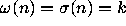 in this case.
in this case.
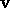
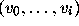
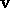
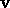

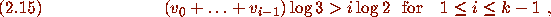 and when (2.15) holds say that
and when (2.15) holds say that 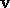 is inflating.
If
is inflating.
If 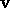 is inflating,
is inflating,
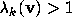 so that
so that 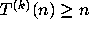 for all n in
for all n in 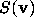 by (2.4),
so that no elements of
by (2.4),
so that no elements of 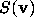 have stopping time k or less.
In the remaining case
have stopping time k or less.
In the remaining case 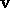 has an initial segment
has an initial segment 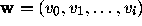 with i < k -1 which is admissible.
Now
with i < k -1 which is admissible.
Now 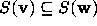 and all sufficiently large elements of
and all sufficiently large elements of
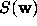 have stopping time i + 1 < k by the argument just given.
have stopping time i + 1 < k by the argument just given.
