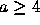 has the property that
has the property that 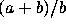 is
a convergent in the continued fraction expansion of
is
a convergent in the continued fraction expansion of 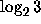 ,
since (2.28) implies that
,
since (2.28) implies that

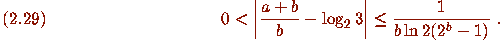 He checks that this rational approximation
He checks that this rational approximation 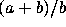 is so good that it
violates the effective estimates of A. Baker [[10], p. 45]
for linear forms in logarithms of algebraic numbers if
is so good that it
violates the effective estimates of A. Baker [[10], p. 45]
for linear forms in logarithms of algebraic numbers if 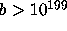 .
Finally he checks that (2.29) fails to hold for all that
.
Finally he checks that (2.29) fails to hold for all that
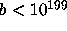 by computing the convergents of the continued fractions
of
by computing the convergents of the continued fractions
of 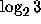 up to
up to 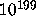 .
.
