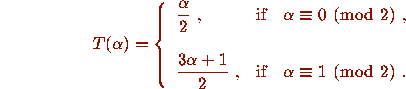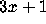 problem has some interesting connections to ergodic theory, because
the function T extends to a measure-preserving function on the 2-adic
integers
problem has some interesting connections to ergodic theory, because
the function T extends to a measure-preserving function on the 2-adic
integers 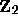 defined with respect to the 2-adic measure.
To explain this, I need some basic facts about the 2-adic integers
defined with respect to the 2-adic measure.
To explain this, I need some basic facts about the 2-adic integers
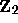 ,
cf. [14], [50].
The 2-adic integers
,
cf. [14], [50].
The 2-adic integers 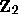 consist of all series
consist of all series

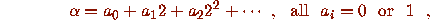 where the
where the 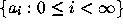 are called the 2- adic digits of
are called the 2- adic digits of 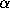 .
One can define congruences
.
One can define congruences 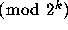 on
on 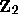 by
by 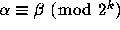 if the first k 2-adic digits of
if the first k 2-adic digits of 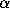 and
and 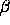 agree.
Addition and multiplication on
agree.
Addition and multiplication on 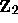 are given by
are given by

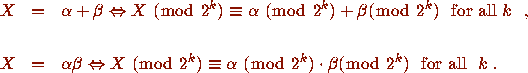 The 2- adic valuation
The 2- adic valuation 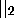 on
on 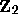 is given by
is given by 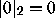 and for
and for
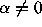 by
by 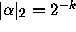 , where
, where 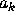 is the
first nonzero 2-adic digit of
is the
first nonzero 2-adic digit of 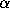 .
The valuation
.
The valuation 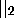 induces a metric d on
induces a metric d on 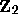 defined by
defined by

 As a topological space
As a topological space 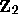 is compact and complete with respect to the metric
d; a basis of open sets for this topology is given by the 2- adic discs of radius
is compact and complete with respect to the metric
d; a basis of open sets for this topology is given by the 2- adic discs of radius
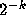 about
about 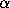 :
:

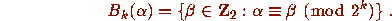 Finally one may consistently define the 2- adic measure
Finally one may consistently define the 2- adic measure
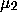 on
on 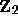 so that
so that

 in particular
in particular 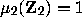 .
The integers
.
The integers  are a subset of
are a subset of 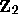 ; for example
; for example

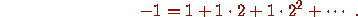 Now one can extend the definition of the function
Now one can extend the definition of the function 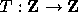 given by (2.1) to
given by (2.1) to 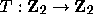 by
by