![[Shownotes]](../gif/annotate/shide-11.gif)
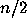 .
The 3x+1 Conjecture asserts that, starting from any positive integer
n, repeated iteration of this function eventually produces the value 1.
.
The 3x+1 Conjecture asserts that, starting from any positive integer
n, repeated iteration of this function eventually produces the value 1.
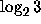 and the distribution
and the distribution 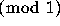 of the sequence
of the sequence
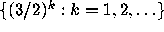 , with questions of ergodic
theory on the 2-adic integers
, with questions of ergodic
theory on the 2-adic integers 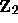 , and with computability theory ---
a generalization of the 3x+1 problem has been shown to be a computationally
unsolvable problem.
In this paper I describe the history of the
, and with computability theory ---
a generalization of the 3x+1 problem has been shown to be a computationally
unsolvable problem.
In this paper I describe the history of the
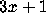 problem and survey all the literature I am aware of
about this problem and its generalizations.
problem and survey all the literature I am aware of
about this problem and its generalizations.

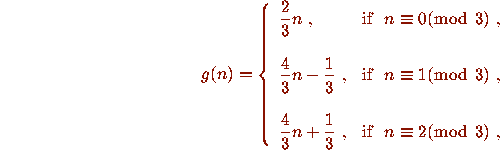 which
gives rise to a permutation P of the natural numbers
which
gives rise to a permutation P of the natural numbers

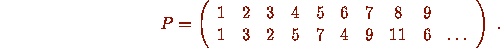 He posed the problem of determining the cycle structure of P, and asked in
particular
whether or not the cycle of this permutation containing 8 is
finite or infinite ,
i.e., whether or not the iterates
He posed the problem of determining the cycle structure of P, and asked in
particular
whether or not the cycle of this permutation containing 8 is
finite or infinite ,
i.e., whether or not the iterates 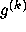 (8) remain
bounded or are unbounded [24].
I will call the study of the iterates of
(8) remain
bounded or are unbounded [24].
I will call the study of the iterates of 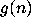 the
original Collatz problem.
Although Collatz never published any of his iteration problems,
he circulated them at the International Congress of
Mathematicians in 1950 in Cambridge,
Massachusetts, and eventually the original Collatz problem appeared in
print ([9], [47], [62]).
His original question concerning
the
original Collatz problem.
Although Collatz never published any of his iteration problems,
he circulated them at the International Congress of
Mathematicians in 1950 in Cambridge,
Massachusetts, and eventually the original Collatz problem appeared in
print ([9], [47], [62]).
His original question concerning 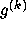 (8) has never been answered;
the cycle it belongs to is believed to be infinite.
Whatever its exact origins, the
(8) has never been answered;
the cycle it belongs to is believed to be infinite.
Whatever its exact origins, the 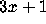 problem was certainly known to the
mathematical community by the early 1950's; it was
discovered in 1952 by B. Thwaites [72].
problem was certainly known to the
mathematical community by the early 1950's; it was
discovered in 1952 by B. Thwaites [72].
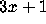 problem has been christened with a variety of names.
Collatz's colleague H. Hasse was interested in the
problem has been christened with a variety of names.
Collatz's colleague H. Hasse was interested in the 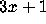 problem and
discussed generalizations of it with many people, leading to the name
Hasse's algorithm [40].
The name Syracuse problem was proposed by Hasse during a visit to
Syracuse University in the 1950's.
Around 1960, S. Kakutani heard the problem, became interested in it,
and circulated it to a number of people.
He said ``For about a month everybody at Yale worked on it,
with no result.
A similar phenomenon happened when I mentioned it at the University of Chicago.
A joke was made that this problem was part of a conspiracy to slow down
mathematical research in the U.S. [45].''
In this process it acquired the name Kakutani's problem.
S. Ulam also heard the problem and circulated the problem at
Los Alamos and elsewhere, and it is called Ulam's problem
in some circles ([13], [72]).
problem and
discussed generalizations of it with many people, leading to the name
Hasse's algorithm [40].
The name Syracuse problem was proposed by Hasse during a visit to
Syracuse University in the 1950's.
Around 1960, S. Kakutani heard the problem, became interested in it,
and circulated it to a number of people.
He said ``For about a month everybody at Yale worked on it,
with no result.
A similar phenomenon happened when I mentioned it at the University of Chicago.
A joke was made that this problem was part of a conspiracy to slow down
mathematical research in the U.S. [45].''
In this process it acquired the name Kakutani's problem.
S. Ulam also heard the problem and circulated the problem at
Los Alamos and elsewhere, and it is called Ulam's problem
in some circles ([13], [72]).
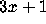 problem has forsaken its underground
existence by appearing in various forms as a problem in books and journals,
sometimes without attribution as an unsolved problem.
Prizes have been offered for its solution:
$50 by H. S. M. Coxeter in 1970, then
$500 by Paul Erdös, and more recently
problem has forsaken its underground
existence by appearing in various forms as a problem in books and journals,
sometimes without attribution as an unsolved problem.
Prizes have been offered for its solution:
$50 by H. S. M. Coxeter in 1970, then
$500 by Paul Erdös, and more recently 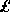 1000 by B. Thwaites [72].
Over twenty research articles have appeared on the
1000 by B. Thwaites [72].
Over twenty research articles have appeared on the 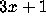 problem and related problems.
problem and related problems.
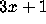 problem itself,
and then discuss generalizations of the problem.
I have included or sketched proofs of Theorems B, D, E, F, M and N
because these results are either new or have not appeared in as sharp a form
previously; the casual reader may skip these proofs.
problem itself,
and then discuss generalizations of the problem.
I have included or sketched proofs of Theorems B, D, E, F, M and N
because these results are either new or have not appeared in as sharp a form
previously; the casual reader may skip these proofs.