



Contents
Next: About this document
Up: No Title
Previous: Conclusion.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-161.gif)
References
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-162.gif)
- 1
-
J.-P. Allouche,
Sur la conjecture de ``Syracuse-Kakutani-Collatz,''
Séminaire de Théorie des Nombres,
1978--1979.
Exp. No. 9, 15, pp.,
CNRS, Talence (France) 1979.
MR 81g:10014.
[1]
- 2
-
Shiro Ando,
letter to J. C. Lagarias, Feb. 18, 1983.
Reports that Prof. Nabuo Yoneda (Dept. of Information Science,
Tokyo Univ.)
has verified the 3x+1 conjecture for all
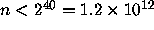 .
.
[1] [2]
- 3
-
R. V. Andrec,
Modern Abstract Algebra,
Holt, Reinhart, and Winston, 1971.
- 4
-
Anon.,
The
 problem.
Popular Computing, 1
(April 1973) 1--2.
problem.
Popular Computing, 1
(April 1973) 1--2.
- 5
-
Anon.,
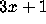 (continued),
Popular Computing, 1 (July 1973) 6--7.
(continued),
Popular Computing, 1 (July 1973) 6--7.
- 6
-
Anon.,
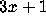 strings, Popular Computing,
2 (April 1973) 12--13.
strings, Popular Computing,
2 (April 1973) 12--13.
- 7
-
Anon.,
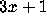 once again,
Popular Computing,
3 (April 1975) 4--5.
once again,
Popular Computing,
3 (April 1975) 4--5.
- 8
-
R. Ash, Information Theory, Interscience Publishers,
Wiley, New York, 1965.
[1]
- 9
-
A. O. L. Atkin,
Comment on Problem 63--13,
SIAM Review, 8 (1966) 234--236.
[1]
- 10
-
A. Baker,
Transcendental Number Theory,
Cambridge Univ. Press, 1975.
[1] [2]
- 11
-
M. Beeler, W. Gosper, R. Schroeppel,
HAKMEM,
Memo 239, Artificial Intelligence Laboratory, M.I.T. 1972,
p. 64.
Presents some numerical results on cycles for the
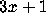 and related problems.
and related problems.
- 12
-
J. Blazewicz and A. Pettorossi,
Collatz's Conjecture and Binary Sequences,
Institute of Control Engineering, Technical University of Poznan,
Poznan, Poland (preprint) March 1983.
- 13
-
C. Böhm and G. Sontacchi,
On the existence of cycles of given length in integer sequences like
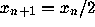 if
if 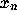 even, and
even, and 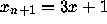 otherwise,
Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis.
Mat. Natur., 64 (1978)
260--264, MR 83h.10030.
otherwise,
Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis.
Mat. Natur., 64 (1978)
260--264, MR 83h.10030.
[1] [2] [3] [4]
- 14
-
Z. I. Borevich and I. R. Shafarevich,
Number Theory, Academic Press, New York, 1966.
[1]
- 15
-
M. J. Bruce, Crazy roller coaster,
Math. Teacher, 71 (January 1978) 45--49.
- 16
-
G. Choquet, Répartition des nombres
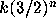 ;
mesures et ensembles associés,
C. R. Acad. Sci. Paris, 290 (31 mars 1980) 575--580.
;
mesures et ensembles associés,
C. R. Acad. Sci. Paris, 290 (31 mars 1980) 575--580.
[1]
- 17
-
,
Algorithmes adaptés aux suites
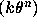 et aux chaines
associées,
C. R. Acad. Sci. Paris,
290 (28 avril 1980) 719--724.
et aux chaines
associées,
C. R. Acad. Sci. Paris,
290 (28 avril 1980) 719--724.
- 18
-
,
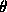 -Jeux récursifs et application aux suites
-Jeux récursifs et application aux suites 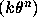 ;
solénoïdes de II
;
solénoïdes de II ,
C. R. Acad. Sci. Paris, 290 (19 mai 1980)
863--868.
,
C. R. Acad. Sci. Paris, 290 (19 mai 1980)
863--868.
- 19
-
,
Construction effective de suites
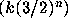 .
Etude des mesures
.
Etude des mesures 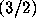 -stables,
C. R. Acad. Sci. Paris, 291 (15 septembre 1980) 69--74.
-stables,
C. R. Acad. Sci. Paris, 291 (15 septembre 1980) 69--74.
- 20
-
,
Les fermés
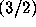 -stables de II;
structure des fermés
dénombrables;
applications arithmétiques,
C. R. Acad. Sci. Paris,
291 (29 septembre 1980) 239--244.
-stables de II;
structure des fermés
dénombrables;
applications arithmétiques,
C. R. Acad. Sci. Paris,
291 (29 septembre 1980) 239--244.
- 21
-
,
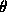 -fermés;
-fermés; 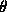 -chaînes et
-chaînes et 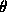 -cycles (pour
-cycles (pour 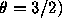 ,
C. R. Acad. Sci. Paris,
292 (5 janvier 1981) 5--10.
,
C. R. Acad. Sci. Paris,
292 (5 janvier 1981) 5--10.
- 22
-
,
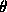 -fermés et dimension de Hausdorff.
Conjecturers de travail.
Arithmétique des
-fermés et dimension de Hausdorff.
Conjecturers de travail.
Arithmétique des 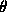 -cycles
(où
-cycles
(où 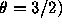 ,
C. R. Acad. Sci. Paris,
292 (9 février 1981) 339--344.
See especially Conjecture D,
which arises from a generalization of the problem
considered by Mahler [49];
cf. (3.4) in the text.
,
C. R. Acad. Sci. Paris,
292 (9 février 1981) 339--344.
See especially Conjecture D,
which arises from a generalization of the problem
considered by Mahler [49];
cf. (3.4) in the text.
[1]
- 23
-
L. Collatz,
letters to R. Terras,
7 May 1976 and 2 Sept. 1976.
- 24
-
,
letter to L. Garner, 17 March 1980.
In none of these letters does L. Collatz
actually state that he proposed the
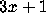 problem.
problem.
[1]
- 25
-
,
Verzweigungsdiagramme und Hypergraphen,
International Series for Numerical Mathematics,
vol. 38,
Birkhäuser, 1977.
This paper remarks on the use of graphical representations to study
iteration problems,
as in Fig. 1 in the text.
It does not discuss the
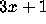 problem.
problem.
[1] [2]
- 26
-
J. H. Conway,
Unpredictable Iterations,
Proc. 1972 Number Theory Conference,
University of Colorado,
Boulder, Colorado (1972) 49--52.
[1]
- 27
-
H. S. M. Coxeter,
Cyclic Sequences and Frieze Patterns
(The Fourth Felix Behrend Memorial Lecture),
1970.
In this lecture Coxeter offered a $50 prize for a proof of the
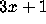 Conjecture and $100 for a counterexample,
according to C. W. Trigg [70].
Conjecture and $100 for a counterexample,
according to C. W. Trigg [70].
- 28
-
R. E. Crandall,
On the ``
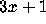 '' problem,
Math. Comp.,
32 (1978) 1281--1292.
'' problem,
Math. Comp.,
32 (1978) 1281--1292.
[1] [2] [3] [4] [5] [6]
- 29
-
J. L. Davidson,
Some Comments on an Iteration Problem,
Proc. 6th Manitoba Conf. on Numerical
Mathematics (1976) 155--159.
[1]
- 30
-
R. Dunn,
On Ulam's Problem,
Dept. of Computer Science Report #CU-CS-011-73, University of
Colorado, Boulder, January 1973.
Reports on computer programs to test the
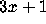 Conjecture and to
calculate the densities
Conjecture and to
calculate the densities 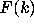 in (2.16) for
in (2.16) for 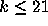 .
.
- 31
-
C. J. Everett, Iteration of the number theoretic function
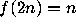 ,
,
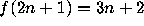 ,
Adv. Math., 25 (1977) 42--45.
,
Adv. Math., 25 (1977) 42--45.
[1]
- 32
-
A. S. Fraenkel, private communication 1981.
[1]
- 33
-
M. Gardner, Mathematical Games,
Scientific American, 226 (June 1972) 114--118.
- 34
-
L. E. Garner, On the Collatz 3n+1 algorithm,
Proc. Amer. Math. Soc.,
82 (1981) 19--22.
[1] [2]
- 35
-
F. Gruenberger,
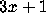 revisited,
Popular Computing,
7 (Oct. 1979) 3--12.
revisited,
Popular Computing,
7 (Oct. 1979) 3--12.
- 36
-
R. K. Guy,
Unsolved Problems in Number Theory,
Springer-Verlag,
New York, 1981 (Problem E16).
[1]
- 37
-
,
Don't try to solve these Problems!,
this MONTHLY, 90 (1983) 35--41.
[1]
- 38
-
,
Conway's prime producing machine,
Math. Mag.,
56 (1983) 26--33.
- 39
-
P. Halmos,
Lectures on Ergodic Theory, Math. Soc. of Japan,
Tokyo,
1956 (Reprint: Chelsea, New York).
[1]
- 40
-
H. Hasse, Unsolved Problems in Elementary Number Theory, Lectures at U.
Maine (Orono),
Spring 1975,
dittoed notes, pp. 23--33.
He states (p. 23) that Thompson has proved the Finite Cycles
Conjecture, a result I am unable to verify.
[1]
- 41
-
E. Heppner,
Eine Bemerkung zum Hasse-Syracuse Algorithmus,
Archiv. Math.,
31 (1978) 317--320,
MR 80d. 10007.
[1] [2]
- 42
-
I. N. Herstein and I. Kaplanaky, Matters Mathematical,
2nd ed.,
Chelsea, New York, 1978,
44--45.
They call the problem the ``Syracuse algorithm.''
- 43
-
D. Hofstadter, Gödel, Escher,
Bach, Basic Books,
New York, 1979.
Brings the
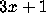 problem to a wide audience by stating it
on pp. 400-402.
problem to a wide audience by stating it
on pp. 400-402.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-163.gif)
- 44
-
S. D. Isard and A. M. Zwicky,
Three open questions in the theory of one-symbol Smullyan systems,
SIGACT News (1969) 11--14.
They propose the problem: Let
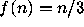 if
if 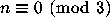 and let
and let 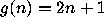 .
Can all numbers
.
Can all numbers 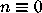 or
or 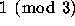 be reduced to 1
by a series of operations f and g?
See [70], p. 148.
be reduced to 1
by a series of operations f and g?
See [70], p. 148.
- 45
-
S. Kakutani, private communication 1981.
[1]
- 46
-
David Kay, Undergraduate Research Project no. 2, Pi Mu Epsilon J.
(1972) 338.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-164.gif)
- 47
-
M. S. Klamkin, Problem 63--12,
SIAM Review, 5 (1963) 275--276.
States the problem:
Consider the permutation
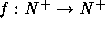 defined by
defined by
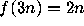 ,
,
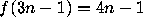 ,
,
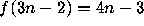 .
Does n = 8 have an infinite trajectory?
How many finite cycles are there for f?
This function was the original one proposed by L. Collatz in 1932
[24].
.
Does n = 8 have an infinite trajectory?
How many finite cycles are there for f?
This function was the original one proposed by L. Collatz in 1932
[24].
[1]
- 48
-
G. M. Leigh and K. R. Matthews,
A generalization of the Syracuse algorithm to
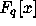 , preprint.
, preprint.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-165.gif)
- 49
-
K. Mahler,
An unsolved problem on the powers of
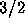 ,
J. Austral. Math. Soc.,
8 (1968) 313--321.
The problem Mahler studies was originally proposed by Prof. Saburô
Uchiyama (Tsukuba Univ.),
according to S. Ando [2].
It arose indirectly in connection with the function
,
J. Austral. Math. Soc.,
8 (1968) 313--321.
The problem Mahler studies was originally proposed by Prof. Saburô
Uchiyama (Tsukuba Univ.),
according to S. Ando [2].
It arose indirectly in connection with the function 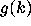 of Waring's
problem, see G. H. Harding and E. M. Wright,
An Introduction to the Theory of Numbers
(4th ed.),
Oxford Univ. Press, 1960, Theorem 393ff.
of Waring's
problem, see G. H. Harding and E. M. Wright,
An Introduction to the Theory of Numbers
(4th ed.),
Oxford Univ. Press, 1960, Theorem 393ff.
[1] [2]
- 50
-
,
P-adic numbers and their functions,
2nd ed.,
Cambridge Univ. Press, 1976.
[1]
- 51
-
K. R. Matthews and A. M. Watts,
A generalization of Hasse's generalization of the Syracuse
algorithm,
Acta. Arith., 43 (1983) 75--83.
[1] [2]
- 52
-
,
A Markov approach to the generalized Syracuse algorithm, preprint.
[1]
- 53
-
,
Some invariant probability measures on the polyadic numbers, preprint.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-166.gif)
- 54
-
H. Möller, Über Hasses Verallgemeinerung des Syracuse-Algorithmus
(Kakutani's Problem),
Acta Arith., 34 (1978)
219--226.
This paper claims A. Fraenkel checked that
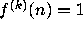 for all
for all 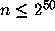 ,
a result in error [32].
In a note added in proof it asserts the proofs of Terras [67]
are faulty.
They seem essentially correct to me, and Terras [68] supplies
elided details.
,
a result in error [32].
In a note added in proof it asserts the proofs of Terras [67]
are faulty.
They seem essentially correct to me, and Terras [68] supplies
elided details.
[1]
- 55
-
J. Nievergelt, J. Farrar, and E. M. Reingold,
Computer Approaches to Mathematical Problems,
Prentice-Hall,
Englewood Cliffs, NJ, 1974, 211-217.
They discuss the problem of checking the
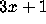 Conjecture for a given
n
and give some interesting empirical observations.
Conjecture for a given
n
and give some interesting empirical observations.
- 56
-
C. Stanley Ogilvy,
Tomorrow's Math,
Oxford Univ. Press, Oxford, 1972, 103.
- 57
-
A. D. Pollington, Intervals Constructions in the Theory of Numbers,
Thesis, University of London, 1980.
See especially Chapter 5, which contains results related to
Mahler's problem [49].
[1]
- 58
-
,
Progressions arithmétiques géneralisées et le problème des
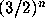 , C. R. Acad. Sci. Paris,
292 (16 février 1981)
383--384.
, C. R. Acad. Sci. Paris,
292 (16 février 1981)
383--384.
[1] [2]
- 59
-
L. Ratzan, Some work on an unsolved palindromic algorithm,
Pi Mu Epsilon J.,
5 (Fall 1973)
463--466.
- 60
-
D. A. Rawsthorne, Imitation of an Iteration, preprint.
- 61
-
B. Schuppar, Kettenbrüche und der 3a+1 Algorithmus, preprint.
[1]
- 62
-
D. Shanks,
Comments on Problem 63--13, SIAM
Review, 7 (1965) 284--286.
Gives the result of a computer search on
Collatz'
original problem (see [9], [47]),
and a heuristic concerning lengths of finite cycles.
[1]
- 63
-
,
Western Number Theory Conference Problem 1975 #5 (R. Guy, ed.)
(mimeographed sheets).
States a conjecture on the average size of the total stopping time function.
[1]
- 64
-
R. P. Steiner,
A Theorem on the Syracuse Problem,
Proc. 7th Manitoba Conference on Numerical Mathematics--1977,
Winnipeg (1978) 553--559.
[1]
- 65
-
,
On the ``Qx+1 Problem,''
Q odd, Fibonacci Quart.,
19 (1981) 285--288.
- 66
-
,
On the ``Qx +1 Problem,''
Q odd II, Fibonacci Quart., 19 (1981) 293--296.
- 67
-
R. Terras,
A stopping time problem on the positive integers,
Acta Arith. 30 (1976) 241--252.
[1] [2] [3] [4] [5] [6]
- 68
-
,
On the existence of a density,
Acta Arith., 35 (1979) 101--102.
[1] [2]
- 69
-
R. Tijdeman,
Det Kongelige Norske Videnskabers Selskak,
Shrifter, 16, 1972.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-167.gif)
- 70
-
C. W. Trigg, C. W. Dodge and L. F. Meyers,
Comments on Problem 133,
Eureka (now Crux Mathematicorum) 2,
no. 7 (August--September 1976) 144--150.
Problem 133 is the
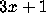 problem, proposed by
K. S. Williams, who said he was shown it by one of his
students.
C. W. Trigg gives a good history of the problem.
problem, proposed by
K. S. Williams, who said he was shown it by one of his
students.
C. W. Trigg gives a good history of the problem.
[1] [2] [3]
- 71
-
M. Vaughan-Lee, letter to L. Garner,
Aug. 10, 1981.
Michael Vaughan-Lee (Oxford U.)
has verified the
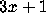 Conjecture for
Conjecture for
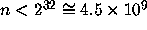 on a Sinclair 2X81 Microcomputer.
on a Sinclair 2X81 Microcomputer.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-168.gif)
- 72
-
C. Williams, B. Thwaites, A. van der Poorten, W. Edwards,
and L. Williams,
Ulam's Conjecture continued again, 1000 pounds for proof.
Rumored proof disclaimed.
References, PPC Calculator J.,
9 (Sept. 1982) 23--24.
Gives some history of the problem.
B. Thwaites states he originated the
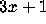 problem in 1952 and offers
1000 pounds for a proof of the
problem in 1952 and offers
1000 pounds for a proof of the 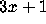 Conjecture.
Conjecture.
[1] [2] [3]
- 73
-
M. Yamada,
A convergence proof about an integral sequence,
Fibonacci Quart.,
18 (1980) 231--242.
The proofs in this paper are incorrect,
see MR 82d:10026.


Contents
Next: About this document
Up: No Title
Previous: Conclusion.
![[Shownotes]](../gif/annotate/shide-161.gif)
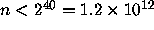 .
. problem.
Popular Computing, 1
(April 1973) 1--2.
problem.
Popular Computing, 1
(April 1973) 1--2.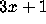 (continued),
Popular Computing, 1 (July 1973) 6--7.
(continued),
Popular Computing, 1 (July 1973) 6--7.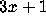 strings, Popular Computing,
2 (April 1973) 12--13.
strings, Popular Computing,
2 (April 1973) 12--13.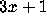 once again,
Popular Computing,
3 (April 1975) 4--5.
once again,
Popular Computing,
3 (April 1975) 4--5.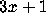 and related problems.
and related problems.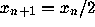 if
if 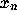 even, and
even, and 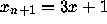 otherwise,
Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis.
Mat. Natur., 64 (1978)
260--264, MR 83h.10030.
otherwise,
Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis.
Mat. Natur., 64 (1978)
260--264, MR 83h.10030.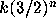 ;
mesures et ensembles associés,
C. R. Acad. Sci. Paris, 290 (31 mars 1980) 575--580.
;
mesures et ensembles associés,
C. R. Acad. Sci. Paris, 290 (31 mars 1980) 575--580.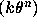 et aux chaines
associées,
C. R. Acad. Sci. Paris,
290 (28 avril 1980) 719--724.
et aux chaines
associées,
C. R. Acad. Sci. Paris,
290 (28 avril 1980) 719--724.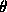 -Jeux récursifs et application aux suites
-Jeux récursifs et application aux suites 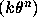 ;
solénoïdes de II
;
solénoïdes de II ,
C. R. Acad. Sci. Paris, 290 (19 mai 1980)
863--868.
,
C. R. Acad. Sci. Paris, 290 (19 mai 1980)
863--868.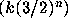 .
Etude des mesures
.
Etude des mesures 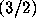 -stables,
C. R. Acad. Sci. Paris, 291 (15 septembre 1980) 69--74.
-stables,
C. R. Acad. Sci. Paris, 291 (15 septembre 1980) 69--74.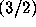 -stables de II;
structure des fermés
dénombrables;
applications arithmétiques,
C. R. Acad. Sci. Paris,
291 (29 septembre 1980) 239--244.
-stables de II;
structure des fermés
dénombrables;
applications arithmétiques,
C. R. Acad. Sci. Paris,
291 (29 septembre 1980) 239--244.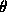 -fermés;
-fermés; 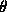 -chaînes et
-chaînes et 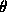 -cycles (pour
-cycles (pour 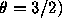 ,
C. R. Acad. Sci. Paris,
292 (5 janvier 1981) 5--10.
,
C. R. Acad. Sci. Paris,
292 (5 janvier 1981) 5--10.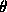 -fermés et dimension de Hausdorff.
Conjecturers de travail.
Arithmétique des
-fermés et dimension de Hausdorff.
Conjecturers de travail.
Arithmétique des 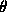 -cycles
(où
-cycles
(où 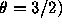 ,
C. R. Acad. Sci. Paris,
292 (9 février 1981) 339--344.
See especially Conjecture D,
which arises from a generalization of the problem
considered by Mahler [49];
cf. (3.4) in the text.
,
C. R. Acad. Sci. Paris,
292 (9 février 1981) 339--344.
See especially Conjecture D,
which arises from a generalization of the problem
considered by Mahler [49];
cf. (3.4) in the text.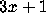 problem.
problem.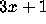 problem.
problem.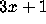 Conjecture and $100 for a counterexample,
according to C. W. Trigg [70].
Conjecture and $100 for a counterexample,
according to C. W. Trigg [70].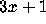 '' problem,
Math. Comp.,
32 (1978) 1281--1292.
'' problem,
Math. Comp.,
32 (1978) 1281--1292.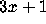 Conjecture and to
calculate the densities
Conjecture and to
calculate the densities 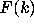 in (2.16) for
in (2.16) for 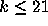 .
.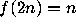 ,
,
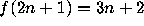 ,
Adv. Math., 25 (1977) 42--45.
,
Adv. Math., 25 (1977) 42--45.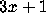 revisited,
Popular Computing,
7 (Oct. 1979) 3--12.
revisited,
Popular Computing,
7 (Oct. 1979) 3--12.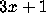 problem to a wide audience by stating it
on pp. 400-402.
problem to a wide audience by stating it
on pp. 400-402.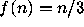 if
if 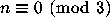 and let
and let 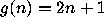 .
Can all numbers
.
Can all numbers 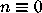 or
or 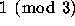 be reduced to 1
by a series of operations f and g?
See [70], p. 148.
be reduced to 1
by a series of operations f and g?
See [70], p. 148.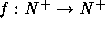 defined by
defined by
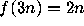 ,
,
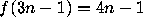 ,
,
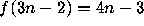 .
Does n = 8 have an infinite trajectory?
How many finite cycles are there for f?
This function was the original one proposed by L. Collatz in 1932
[24].
.
Does n = 8 have an infinite trajectory?
How many finite cycles are there for f?
This function was the original one proposed by L. Collatz in 1932
[24].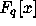 , preprint.
, preprint.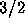 ,
J. Austral. Math. Soc.,
8 (1968) 313--321.
The problem Mahler studies was originally proposed by Prof. Saburô
Uchiyama (Tsukuba Univ.),
according to S. Ando [2].
It arose indirectly in connection with the function
,
J. Austral. Math. Soc.,
8 (1968) 313--321.
The problem Mahler studies was originally proposed by Prof. Saburô
Uchiyama (Tsukuba Univ.),
according to S. Ando [2].
It arose indirectly in connection with the function 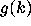 of Waring's
problem, see G. H. Harding and E. M. Wright,
An Introduction to the Theory of Numbers
(4th ed.),
Oxford Univ. Press, 1960, Theorem 393ff.
of Waring's
problem, see G. H. Harding and E. M. Wright,
An Introduction to the Theory of Numbers
(4th ed.),
Oxford Univ. Press, 1960, Theorem 393ff.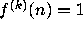 for all
for all 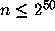 ,
a result in error [32].
In a note added in proof it asserts the proofs of Terras [67]
are faulty.
They seem essentially correct to me, and Terras [68] supplies
elided details.
,
a result in error [32].
In a note added in proof it asserts the proofs of Terras [67]
are faulty.
They seem essentially correct to me, and Terras [68] supplies
elided details.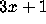 Conjecture for a given
n
and give some interesting empirical observations.
Conjecture for a given
n
and give some interesting empirical observations.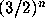 , C. R. Acad. Sci. Paris,
292 (16 février 1981)
383--384.
, C. R. Acad. Sci. Paris,
292 (16 février 1981)
383--384.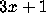 problem, proposed by
K. S. Williams, who said he was shown it by one of his
students.
C. W. Trigg gives a good history of the problem.
problem, proposed by
K. S. Williams, who said he was shown it by one of his
students.
C. W. Trigg gives a good history of the problem.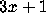 Conjecture for
Conjecture for
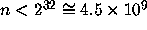 on a Sinclair 2X81 Microcomputer.
on a Sinclair 2X81 Microcomputer.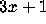 problem in 1952 and offers
1000 pounds for a proof of the
problem in 1952 and offers
1000 pounds for a proof of the 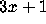 Conjecture.
Conjecture.