The number of nodes in the search tree can often be reduced by using the
symmetry or property-preserving operations. If A is the
incidence matrix of a projective plane, then the operations of permuting
the rows and permuting the columns of A correspond only to reordering
the lines and points of the plane. These operations preserve the property
of being a projective plane. To see how they reduce the size of a search
tree, consider the plane of order 10. There are
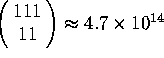 choices for the first column, corresponding to the number of ways of
placing 11 ones in the 111 rows. By using the row permutations, we can
assume that all these ones are placed on the first 11 rows, reducing the
number of partial solutions
choices for the first column, corresponding to the number of ways of
placing 11 ones in the 111 rows. By using the row permutations, we can
assume that all these ones are placed on the first 11 rows, reducing the
number of partial solutions 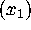 from
from 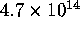 to 1.
Mathematicians love to use the phrase ``without loss of generality'' to
indicate a simplification by symmetry operations. So without loss of
generality, the second column has only one choice --- with a one in the
first row and the remaining 10 ones in rows 12 to 21. Now, row 1 has nine
remaining ones. By permuting columns, we can assume that these remaining
ones of row 1 are in columns 3 to 11. Next, by row permutation, the
remaining 10 ones of column 3 can be placed in rows 22 to 31. Continuing
in this manner, it is not difficult to show that there is only one choice
up to column 21. Beyond this point, symmetry operations are difficult to
visualize, because they often involve combinations of row and column
permutations.
to 1.
Mathematicians love to use the phrase ``without loss of generality'' to
indicate a simplification by symmetry operations. So without loss of
generality, the second column has only one choice --- with a one in the
first row and the remaining 10 ones in rows 12 to 21. Now, row 1 has nine
remaining ones. By permuting columns, we can assume that these remaining
ones of row 1 are in columns 3 to 11. Next, by row permutation, the
remaining 10 ones of column 3 can be placed in rows 22 to 31. Continuing
in this manner, it is not difficult to show that there is only one choice
up to column 21. Beyond this point, symmetry operations are difficult to
visualize, because they often involve combinations of row and column
permutations.
 Annotation Form Interface
Annotation Form Interface
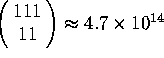 choices for the first column, corresponding to the number of ways of
placing 11 ones in the 111 rows. By using the row permutations, we can
assume that all these ones are placed on the first 11 rows, reducing the
number of partial solutions
choices for the first column, corresponding to the number of ways of
placing 11 ones in the 111 rows. By using the row permutations, we can
assume that all these ones are placed on the first 11 rows, reducing the
number of partial solutions 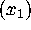 from
from 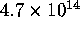 to 1.
Mathematicians love to use the phrase ``without loss of generality'' to
indicate a simplification by symmetry operations. So without loss of
generality, the second column has only one choice --- with a one in the
first row and the remaining 10 ones in rows 12 to 21. Now, row 1 has nine
remaining ones. By permuting columns, we can assume that these remaining
ones of row 1 are in columns 3 to 11. Next, by row permutation, the
remaining 10 ones of column 3 can be placed in rows 22 to 31. Continuing
in this manner, it is not difficult to show that there is only one choice
up to column 21. Beyond this point, symmetry operations are difficult to
visualize, because they often involve combinations of row and column
permutations.
to 1.
Mathematicians love to use the phrase ``without loss of generality'' to
indicate a simplification by symmetry operations. So without loss of
generality, the second column has only one choice --- with a one in the
first row and the remaining 10 ones in rows 12 to 21. Now, row 1 has nine
remaining ones. By permuting columns, we can assume that these remaining
ones of row 1 are in columns 3 to 11. Next, by row permutation, the
remaining 10 ones of column 3 can be placed in rows 22 to 31. Continuing
in this manner, it is not difficult to show that there is only one choice
up to column 21. Beyond this point, symmetry operations are difficult to
visualize, because they often involve combinations of row and column
permutations.