![[Shownotes]](../gif/annotate/sshow-51.gif)
We realised also that it is important to estimate how long a computer
search would take. It would be useless to speed up a program by a factor
of ten, if the resulting program still requires 100 years to run. However,
speeding it up by a factor of 1000 would make the search feasible in our
environment. By adapting Knuth's Monte Carlo method [16], we
estimated that the search tree had about 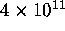 nodes. Hoping
that we could process
nodes. Hoping
that we could process 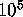 nodes per second, we arrived at an estimate
of 50 days of computer time.
nodes per second, we arrived at an estimate
of 50 days of computer time.
I was going to present the final results at the Ninth Australian
Conference on Combinatorial Mathematics in 1981, but the program
development was slower than expected. At the conference, I had to quickly
change my plan and talked about a feasibility study of such a search
[17]. The program was finally developed and the search finished
late in 1982. We did not find a completed incidence matrix and so, 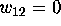 [18]. Ryser was happy with the result and encouraged us to
continue. Hall was both excited and pessimistic. He wrote, ``For the first
time, I doubt that a plane of order 10 exists.''
[18]. Ryser was happy with the result and encouraged us to
continue. Hall was both excited and pessimistic. He wrote, ``For the first
time, I doubt that a plane of order 10 exists.''
The search for weight 12 codewords took 183 days instead of the predicted
50. The main reason for the discrepancy was that we could process only
about 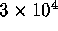 nodes per second instead of
nodes per second instead of 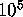 . Yet, we learned
a lot about the planning of the search, the estimation process, and the
optimization techniques --- knowledge which became useful in our later
programs. In retrospect, we probably could have reduced the size of the
search tree by another factor of 10 and come within the predicted time.
. Yet, we learned
a lot about the planning of the search, the estimation process, and the
optimization techniques --- knowledge which became useful in our later
programs. In retrospect, we probably could have reduced the size of the
search tree by another factor of 10 and come within the predicted time.
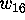 and then the weight enumerator. Unless the weight
enumerator provides a contradiction, we still have to perform another
search. Hall in [14] proved that if
and then the weight enumerator. Unless the weight
enumerator provides a contradiction, we still have to perform another
search. Hall in [14] proved that if 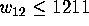 ,
then there exist primitive weight 20 codewords,
which intersect the lines of the plane in at most four points.
We might be able to skip
the step of finding
,
then there exist primitive weight 20 codewords,
which intersect the lines of the plane in at most four points.
We might be able to skip
the step of finding 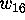 if we could go directly to weight 20.
Unfortunately, we obtained an estimate of at least
if we could go directly to weight 20.
Unfortunately, we obtained an estimate of at least 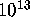 weight 20
starting configurations. Even though, as Hall remarked, it required only a
few minutes of computer time to try each starting configuration, a few
minutes times
weight 20
starting configurations. Even though, as Hall remarked, it required only a
few minutes of computer time to try each starting configuration, a few
minutes times 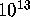 equaled
equaled 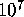 years --- clearly beyond our
capability. There was no short cut which could avoid computing the weight
enumerator.
years --- clearly beyond our
capability. There was no short cut which could avoid computing the weight
enumerator.
During my visit to the University of Cambridge in 1982, Thompson showed me Carter's thesis and suggested that we might be able to finish the remaining cases. It was the first time I read his thesis and I was surprised by how familiar his computing techniques were. We had rediscovered a lot of what was already in his thesis! Thompson also made me promise to redo Carter's work on weight 16, just to have an independent verification of its correctness. Although I have yet to do it, I still intend to fulfil this promise.
In the mean time, Larry had developed an extremely useful prototyping program, called NPL. It had a very humble beginning. Working with incidence matrices meant that we often had to draw them and fill in large numbers of zeros and ones. As a labour saving move, we started drawing templates and then making photocopies. Larry took this one step further, printing the matrices with a computer rather than drawing the templates by hand. Soon we included the capability of initializing the starting configurations and later, the ability to backtrack was also included. Before long, it became a full-blown prototyping program, capable of performing estimations and adapting to new configurations. It turned out to be an extremely useful tool. We could quickly explore an idea for an ``improvement'' to the search. Ideas that turned out to increase the required CPU time were discarded. We could use it to plan our final search in detail, without having to write the program first. The most exciting stage was this planning stage.
Using NPL, we found a feasible way to solve the remaining cases of Carter.
Compared to Carter's work, we found a better search order and a better use
of the symmetry, both reducing the size of the search tree.
Carefully optimised programs to implement the planned attack were written
for each of the remaining cases. Running on two VAX computers, it took the
equivalent of 80 days of computing on a VAX-11/780 [19]. No
completed incidence matrix was found and hence 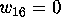 .
Now that
.
Now that 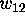 ,
, 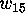 and
and 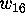 were all known to be zero, we
could compute the weight enumerator of the binary error-correcting code
for the plane of order 10 [20]. What catches the eye is that
were all known to be zero, we
could compute the weight enumerator of the binary error-correcting code
for the plane of order 10 [20]. What catches the eye is that
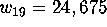 . If one follows the same method of finding starting
configurations and trying to extend them, then one will either construct
the plane or show that it does not exist.
. If one follows the same method of finding starting
configurations and trying to extend them, then one will either construct
the plane or show that it does not exist.
By simple counting arguments, 17 of the 66 cases can easily be eliminated. Four other cases are eliminated in a more ad hoc manner. Scott Crossfield, working with me as an NSERC Summer Undergraduate Assistant, obtained estimates for each of the remaining 45 cases. Our preliminary results indicated that the problem could be solved with another two years of computing time. These arguments and estimation results were presented in [19].
We decided to solve these cases by starting from the easy ones and hoping to discover better methods for the more difficult ones. We hedged our preliminary estimates by saying that it might be too optimistic. Our estimate of how fast the computer could test the acceptability of a column was based on our experience of the weight 12 and 16 cases. For weight 19, this test was much slower for technical reasons which were related to the fact that 19 is an odd number whereas the other two numbers are even. We could proceed only about 60 nodes per second, giving an estimate of 100 years to finish the search. To make the search feasible, we needed to speed it up by another factor of 100. The only possibility left was to use a faster computer, bringing to mind a supercomputer. Fortunately, our method could be easily adapted to use the vectoring capability of a supercomputer [31]. It was time to ask for help. Both Hall and Thompson suggested that IDA might be willing because it had helped Carter previously. After some discussion with Nick Patterson, the deputy director of the Communication Research Division at IDA, he agreed to run our yet undeveloped program on their CRAY-1A as the lowest priority job using up the otherwise idling computer. He and Douglas Wiedemann, who was on leave from IDA pursuing graduate studies at the University of Waterloo, gave us many suggestions on the efficient usage of the CRAY. In addition, Patterson looked after the day-to-day running of the program for over two years. He was the unsung hero in the successful completion of our work.
In the mean time, Concordia had acquired more and more VAX computers. Soon, we were running our program on five different computers. We figured that there was enough computing resources at Concordia to solve all but a few of the most difficult cases. So we targeted the CRAY program for only one type of starting configuration which contained all the most difficult cases. The other configurations were left for our VAX computers to solve. All the cases at Concordia finished around January 1987 and took the equivalent of 800 days of VAX-11/780 computer time.
In order to avoid any unpleasant surprises involved in running programs at
a long distance, we also put in a number of safety checks. Most of them
were related to testing whether the sizes of the internal data structures
were large enough. For lack of memory space, one could not merely allocate
the largest expected size for every structure. Instructions were given on
how to selectively increase the sizes. Some data structures were so
specialized that their size could not be increased. We temporarily ignored
the problem by deciding to handle them later, if necessary. Of course, we
hoped that it would not be necessary.
We finished developing our CRAY program in 1986 and we were relieved to
obtain a final estimate of about 3 months of CRAY computer time. It
started running at IDA in the fall of 1986 and was to await completion in
two to three years.