



Contents
Next: Epilogue
Up:The Search for a
Previous: The Finish Line
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-71.gif)
This is not the first time that a computer has played an important role in
``proving'' a theorem. A notable earlier example is the four-color theorem
[3]. Yet, these are not proofs in the traditional mathematical
sense. It is impossible for any human being to check through all the
calculations. From personal experience, it is extremely easy to make
programming mistakes. We have taken many precautions, including the use of
two different programs to cross check selective sample cases and the
checking of internal consistency when isomorphism testing is performed.
Yet, I want to emphasize that this is only an experimental result and it
desperately needs an independent verification, or better still, a
theoretical explanation.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-72.gif)
There is, moreover, the possibility of an undetected hardware failure. A
common error of this type is the random changing of bits in a computer
memory, which could mean the loss of a branch of the search tree. This is
the worst kind of hardware error, because we might loose solutions without
realizing it. The CRAY-1A is reported to have such errors at the rate of
about one per one thousand hours of computing. At this rate, we expect to
encounter two to three errors! We did discover one such error by chance.
After a hardware problem, Patterson reran the 1,000 A2's just before the
failure and the statistics have changed for the A2 processed just prior
to the malfunction. How should one receive a ``proof'' that is almost
guaranteed to contain several random errors?
[an error occurred while processing this directive]
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-73.gif)
Unfortunately, this is an unavoidable nature of a computer-based proof ---
it is never absolute. However, despite this reservation, we argued in
[21] that the possibility of hardware errors leading us to a wrong
conclusion is extremely small. Since each A2 is in a separate run and
there are about half a million non-isomorphic A2's, the probability of
one random hardware error affecting one specific A2 is about 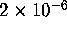 . Suppose we accept that the weight enumerator is correct. Then if
an undiscovered plane of order 10 exists, it would contain 24,675 weight
19 codewords. The 19 points in each such codeword give rise to an A2.
Since we have searched through all non-isomorphic A2's, we must have
encountered these special A2's. If all these 24,675 special A2's are
isomorphic, then only one out of about half a million non-isomorphic
A2's can be extended to the undiscovered plane. Even under this
assumption, the probability of this special A2 being affected by two or
three undetected hardware errors is less than
. Suppose we accept that the weight enumerator is correct. Then if
an undiscovered plane of order 10 exists, it would contain 24,675 weight
19 codewords. The 19 points in each such codeword give rise to an A2.
Since we have searched through all non-isomorphic A2's, we must have
encountered these special A2's. If all these 24,675 special A2's are
isomorphic, then only one out of about half a million non-isomorphic
A2's can be extended to the undiscovered plane. Even under this
assumption, the probability of this special A2 being affected by two or
three undetected hardware errors is less than 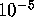 . Is it likely that
all 24,675 A2's arising from an undiscovered plane are isomorphic? Since
the plane is known to have a trivial collineation group
[1,15,36], it is more likely that there are two
or more non-isomorphic A2's amongst the 24,675 cases. In this situation,
the probability of hardware errors affecting all of them is infinitesimal.
The same argument can be used even if we do not assume the correctness of
previous computer-based results. Basically, the argument depends on the
observation that if a plane of order 10 exists, then it can be constructed
from many different starting points. Random hardware failures are unlikely
to eliminate all of them. In other words, the fact that no one has yet
constructed one is a very strong indication that it does not exist.
. Is it likely that
all 24,675 A2's arising from an undiscovered plane are isomorphic? Since
the plane is known to have a trivial collineation group
[1,15,36], it is more likely that there are two
or more non-isomorphic A2's amongst the 24,675 cases. In this situation,
the probability of hardware errors affecting all of them is infinitesimal.
The same argument can be used even if we do not assume the correctness of
previous computer-based results. Basically, the argument depends on the
observation that if a plane of order 10 exists, then it can be constructed
from many different starting points. Random hardware failures are unlikely
to eliminate all of them. In other words, the fact that no one has yet
constructed one is a very strong indication that it does not exist.


Contents
Next: Epilogue
Up:The Search for a
Previous: The Finish Line
[an error occurred while processing this directive]
![[Shownotes]](../gif/annotate/shide-71.gif)
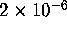 . Suppose we accept that the weight enumerator is correct. Then if
an undiscovered plane of order 10 exists, it would contain 24,675 weight
19 codewords. The 19 points in each such codeword give rise to an A2.
Since we have searched through all non-isomorphic A2's, we must have
encountered these special A2's. If all these 24,675 special A2's are
isomorphic, then only one out of about half a million non-isomorphic
A2's can be extended to the undiscovered plane. Even under this
assumption, the probability of this special A2 being affected by two or
three undetected hardware errors is less than
. Suppose we accept that the weight enumerator is correct. Then if
an undiscovered plane of order 10 exists, it would contain 24,675 weight
19 codewords. The 19 points in each such codeword give rise to an A2.
Since we have searched through all non-isomorphic A2's, we must have
encountered these special A2's. If all these 24,675 special A2's are
isomorphic, then only one out of about half a million non-isomorphic
A2's can be extended to the undiscovered plane. Even under this
assumption, the probability of this special A2 being affected by two or
three undetected hardware errors is less than 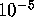 . Is it likely that
all 24,675 A2's arising from an undiscovered plane are isomorphic? Since
the plane is known to have a trivial collineation group
[1,15,36], it is more likely that there are two
or more non-isomorphic A2's amongst the 24,675 cases. In this situation,
the probability of hardware errors affecting all of them is infinitesimal.
The same argument can be used even if we do not assume the correctness of
previous computer-based results. Basically, the argument depends on the
observation that if a plane of order 10 exists, then it can be constructed
from many different starting points. Random hardware failures are unlikely
to eliminate all of them. In other words, the fact that no one has yet
constructed one is a very strong indication that it does not exist.
. Is it likely that
all 24,675 A2's arising from an undiscovered plane are isomorphic? Since
the plane is known to have a trivial collineation group
[1,15,36], it is more likely that there are two
or more non-isomorphic A2's amongst the 24,675 cases. In this situation,
the probability of hardware errors affecting all of them is infinitesimal.
The same argument can be used even if we do not assume the correctness of
previous computer-based results. Basically, the argument depends on the
observation that if a plane of order 10 exists, then it can be constructed
from many different starting points. Random hardware failures are unlikely
to eliminate all of them. In other words, the fact that no one has yet
constructed one is a very strong indication that it does not exist.