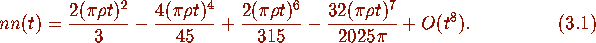We have computed many terms of the power series expansion of (2.7) about s=0 with b=1 and subject to (2.8). Substitution of the first seven into (2.4) gives

Comparison with the analogous expansion of (1.3a) (see e.g. [2]) shows that 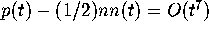, which in qualitative terms says that very small spacings between consecutive eigenvalues will most likely be nearest neighbour spacings (the factor of 1/2 accounts for the fact that the nearest neighbour occurs with equal probability to the left or the right).
Annotation Form Interface

          Your name: 
     E-Mail address: 
 Annotation Subject: 
        Related URL: