![[Shownotes]](../gif/annotate/sshow-11.gif)
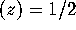 have the
same joint distribution as that of the eigenvalues of a random matrix from
the Gaussian Unitary Ensemble (GUE) of large (formally infinite) dimensional
random Hermitian matrices. Denoting the zeros by
have the
same joint distribution as that of the eigenvalues of a random matrix from
the Gaussian Unitary Ensemble (GUE) of large (formally infinite) dimensional
random Hermitian matrices. Denoting the zeros by 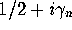 , where n
labels the zeros sequentially along the critical line, the GUE hypothesis
applies in the limit
, where n
labels the zeros sequentially along the critical line, the GUE hypothesis
applies in the limit 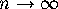 , with each
, with each 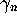 scaled by the
mean density of zeros at
scaled by the
mean density of zeros at 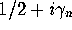
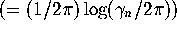 , so that the mean spacing between zeros is unity (any finite value will
do).
We recall (see e.g. [2]) that a random Hermitian
, so that the mean spacing between zeros is unity (any finite value will
do).
We recall (see e.g. [2]) that a random Hermitian 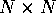 matrix is said to
belong to the GUE if the diagonal elements
matrix is said to
belong to the GUE if the diagonal elements 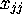 (which must be real) and the
upper triangular elements
(which must be real) and the
upper triangular elements 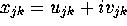 are independently chosen
with probability density function (p.d.f.)
are independently chosen
with probability density function (p.d.f.)

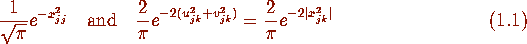 respectively. For large N the density of eigenvalues
respectively. For large N the density of eigenvalues 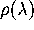 is given by the so
called Wigner semi-circle law
is given by the so
called Wigner semi-circle law

 To apply the GUE hypothesis the eigenvalues should therefore be scaled by
To apply the GUE hypothesis the eigenvalues should therefore be scaled by
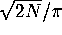 before the
before the 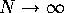 is taken, to obtain a
mean eigenvalue spacing of unity.
is taken, to obtain a
mean eigenvalue spacing of unity.
One consequence of the GUE hypothesis is that it provides concrete predictions
for statistical properties of 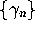 , whenever these are known for
the GUE random matrices. One such example is the p.d.f.,
, whenever these are known for
the GUE random matrices. One such example is the p.d.f., 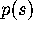 say, for the
spacing between consecutive zeros. In the infinite GUE, scaled so that
the mean eigenvalue spacing is
say, for the
spacing between consecutive zeros. In the infinite GUE, scaled so that
the mean eigenvalue spacing is 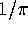 , the corresponding quantity is given in
terms of a Fredholm determinant of an integral operator (see e.g. [2]) by
, the corresponding quantity is given in
terms of a Fredholm determinant of an integral operator (see e.g. [2]) by

 where K is the integral operator on the interval
where K is the integral operator on the interval 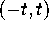 with kernel
with kernel

 Using an eigenvalue expansion of the Fredholm determinant,
Using an eigenvalue expansion of the Fredholm determinant, 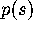 can be
computed [3] (see also [1]) to give a tabulation or graph of
can be
computed [3] (see also [1]) to give a tabulation or graph of 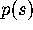 .
.
In a large-scale numerical computation of the non-trivial zeros of the Riemann
zeta function by one of the present authors [1], involving over 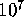 consecutive values of
consecutive values of 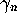 about
about 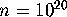 calculated to an
accuracy of about six decimal places, the p.d.f.
calculated to an
accuracy of about six decimal places, the p.d.f. 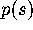 has been determined
empirically and compared with
has been determined
empirically and compared with 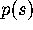 as calculated from (1.3). Excellent
agreement is found. Similar agreement is found when comparing other empirical
statistical distributions with those known exactly for the GUE.
as calculated from (1.3). Excellent
agreement is found. Similar agreement is found when comparing other empirical
statistical distributions with those known exactly for the GUE.
In this paper we present the exact calculation of a new statistical quantity
for the infinite GUE, which is similar in meaning to 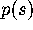 . This statistical
quantity is the p.d.f.,
. This statistical
quantity is the p.d.f., 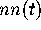 say, for the spacing between nearest neighbor
eigenvalues. We then test the GUE hypothesis by comparing
say, for the spacing between nearest neighbor
eigenvalues. We then test the GUE hypothesis by comparing 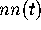 for the
infinite GUE with the empirical calculation of
for the
infinite GUE with the empirical calculation of 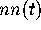 for the zeros the
Riemann zeta function on the critical line from the data of [1] for
for the zeros the
Riemann zeta function on the critical line from the data of [1] for
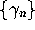 .
.