---

---

---

Contents Next: 2.2 Derivation Up: 2. A NON-LINEAR Previous: 2. A NON-LINEAR

---

---

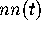So as to put our calculation of in context, we first note that the expression (1.3) for 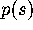has been made more explicit by Jimbo et al. [4], who proved that

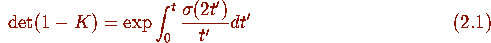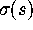where satisfies the 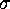form of the Painlevé V equation:

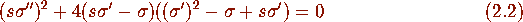subject to the boundary condition

Subsequent derivations of this result have been given by Its et al. [5], Mehta [6] and Tracy and Widom [7]. Our expression for 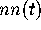is given in terms of the solution of a non-linear equation which generalizes (2.2).

---

---

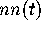We have obtained the following results. The p.d.f. for the infinite GUE is given in terms of a Fredholm determinant by

where 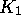is the integral operator on 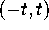with kernel

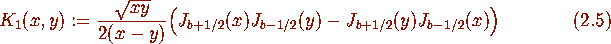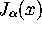( denotes the Bessel function) and b=1. Furthermore

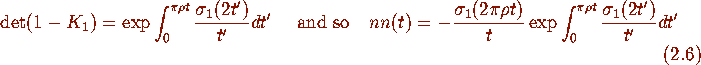(here the mean eigenvalue spacing is 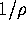), where 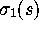satisfies the non-linear equation

with b=1, subject to the boundary condition

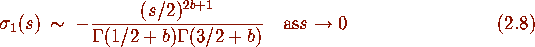with b=1 (the parameter b is included above for later convenience). Note that with b=0 (2.7) reduces to (2.2).

---

---

omp@cecm.sfu.ca