![[Shownotes]](../gif/annotate/shide-41.gif)

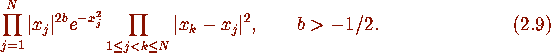 They prove that in the thermodynamic limit, with each
They prove that in the thermodynamic limit, with each 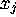 scaled
scaled
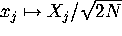 so that the bulk density is
so that the bulk density is 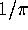 , the
corresponding n-particle distribution is given by
, the
corresponding n-particle distribution is given by

 where
where 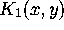 is given by (2.5) (for
is given by (2.5) (for 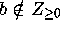 ,
, 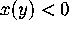 ,
,
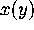 in the denominator needs to be replaced by
in the denominator needs to be replaced by 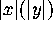 , however below
we will only consider the case
, however below
we will only consider the case 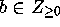 ).
).

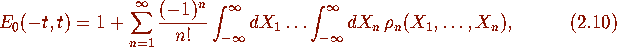 where
where 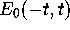 denotes the probability of an interval
denotes the probability of an interval
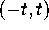 being free of eigenvalues in the ensemble (2.9), that
being free of eigenvalues in the ensemble (2.9), that

 Since in the case b=1 (2.9) is precisely the eigenvalue
probability density function of the GUE with an eigenvalue fixed at the
origin, the result (2.4) follows.
Since in the case b=1 (2.9) is precisely the eigenvalue
probability density function of the GUE with an eigenvalue fixed at the
origin, the result (2.4) follows.
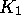 . To present these equations, the
particular quantities must first be defined.
. To present these equations, the
particular quantities must first be defined.
Definition 2.1
Suppose A is an integral operator on the interval 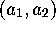 with kernel
with kernel
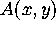 :
:

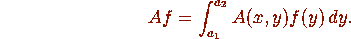 We write
We write

 to specify that the kernel of A is
to specify that the kernel of A is 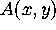 . Denote by K an integral
operator of this type with kernel of the form
. Denote by K an integral
operator of this type with kernel of the form

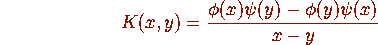 and write
and write

 Also let
Also let

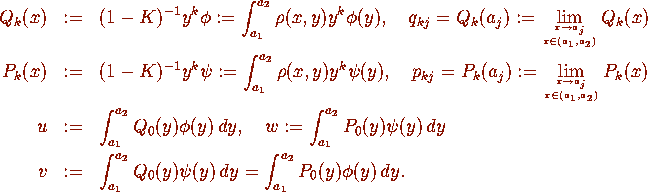 where k=0,1 and j=1,2.
where k=0,1 and j=1,2.
The coupled equations which imply (2.7) can now be stated.
Proposition 2.1
Consider the kernel (2.5) with 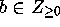 on
on 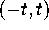 so that in the
setting of Definition 2.1
so that in the
setting of Definition 2.1 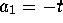 and
and 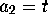 . With the notation
. With the notation
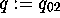 ,
, 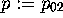 ,
, 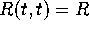 we have
we have

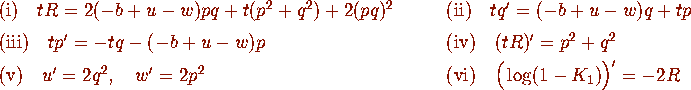 where the dashes denote differentiation with respect to t.
The theory of Tracy and Widom [9] allows equations for the quantities of
Definition 2.1 to be derived which imply the equations of Proposition 2.1.
Before presenting these equations let us show how (2.6) and
(2.7) can be derived from
the equations of Proposition 2.1.
where the dashes denote differentiation with respect to t.
The theory of Tracy and Widom [9] allows equations for the quantities of
Definition 2.1 to be derived which imply the equations of Proposition 2.1.
Before presenting these equations let us show how (2.6) and
(2.7) can be derived from
the equations of Proposition 2.1.
First consider (2.7). We multiply (ii) by p, multiply (iii) by q, add and use (v) to obtain

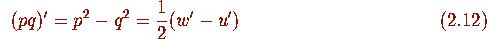 and consequently
and consequently

 Substituting (3.2) and (iv) in (i) gives
Substituting (3.2) and (iv) in (i) gives

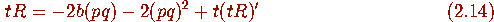 which relates tR to pq. On the other hand, another equation relating these
two quantities is obtained by squaring (iv) and the first equality in (2.12)
and subtracting:
which relates tR to pq. On the other hand, another equation relating these
two quantities is obtained by squaring (iv) and the first equality in (2.12)
and subtracting:

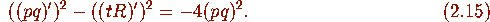 Solving (2.14) for pq (it follows from a
small-t expansion that the negative square root is to be taken) and
Solving (2.14) for pq (it follows from a
small-t expansion that the negative square root is to be taken) and 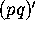 ,
substituting in (2.15) and introducing the notation
,
substituting in (2.15) and introducing the notation

 gives (2.7).
The boundary condition (2.8) follows from the fact that
gives (2.7).
The boundary condition (2.8) follows from the fact that 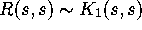 as
as 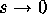 and the corresponding behaviour of
and the corresponding behaviour of 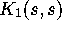 deduced from (7).
deduced from (7).
To derive (2.6) we simply substitute (2.16) in (vi) and integrate. The factor
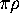 in the upper terminal of (2.6) results from changing
the mean eigenvalue spacing from
in the upper terminal of (2.6) results from changing
the mean eigenvalue spacing from 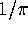 to
to 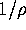 .
.