![[Shownotes]](../gif/annotate/shide-51.gif)
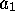 ,
, 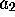 . These equations are of two types:
those which apply independent of the particular functions
. These equations are of two types:
those which apply independent of the particular functions 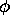 and
and
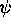 , and those which are dependent on
, and those which are dependent on 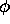 and
and 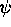 .
.
For general values of 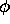 and
and 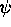 in Definition 2.1 we have
in Definition 2.1 we have

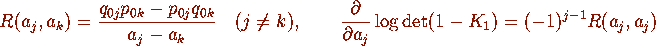 and
and

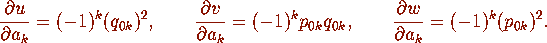 where j,k = 1,2.
To present the second type of equations, note that the kernel
where j,k = 1,2.
To present the second type of equations, note that the kernel 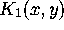 as
given by (2.5) is of the type in Definition 2.1 with
as
given by (2.5) is of the type in Definition 2.1 with

 In [9] Tracy and Widom show that equations further to those in Proposition
2.3 exist whenever
In [9] Tracy and Widom show that equations further to those in Proposition
2.3 exist whenever 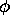 and
and 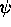 satisfy the coupled differential equations
satisfy the coupled differential equations

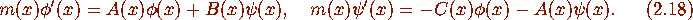 for m,A,B,C polynomials. For the choice (2.6), (2.7) hold with
for m,A,B,C polynomials. For the choice (2.6), (2.7) hold with

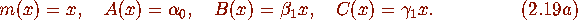 with
with


For general 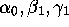 we can read off from the results of
[9] additional equations relating the quantities
we can read off from the results of
[9] additional equations relating the quantities 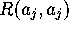 ,
, 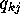 ,
,
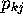 (
(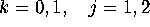 ) and u,v,w.
) and u,v,w.
Proposition 2.4
Consider the kernel K of Definition 2.1 with 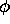 and
and 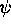 defined by
(2.18) with m,A,B,C as in (2.19a). We have
defined by
(2.18) with m,A,B,C as in (2.19a). We have





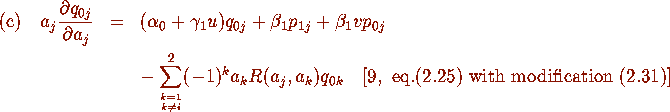

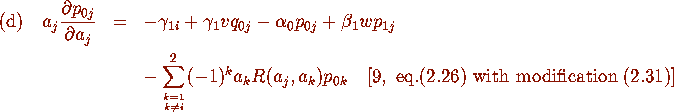

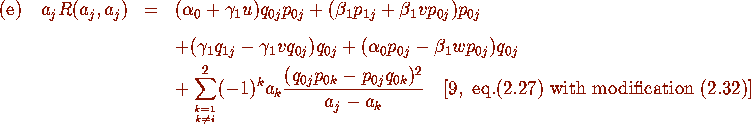

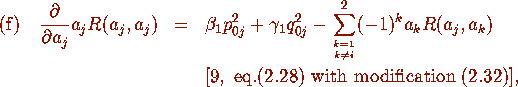 where j=1,2.
To pursue our task of deriving the equations in Proposition 2.1, let us return
to the particular case
where j=1,2.
To pursue our task of deriving the equations in Proposition 2.1, let us return
to the particular case

 and
and 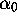 ,
, 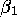 ,
, 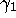 given by (2.8b) so that
given by (2.8b) so that 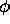 and
and 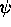 are given by (2.6). Since
are given by (2.6). Since

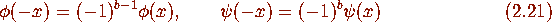 (recall
(recall 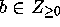 ) we have
) we have 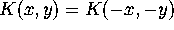 and thus
and thus 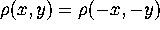 , which together with (2.21) implies
, which together with (2.21) implies

 With the aid of (2.22) the equations in Proposition 2.1 can now be deduced in
a straightforward manner from the equations in Proposition 2.3 and 2.4.
With the aid of (2.22) the equations in Proposition 2.1 can now be deduced in
a straightforward manner from the equations in Proposition 2.3 and 2.4.
We first use (a) and (b) to eliminate 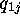 and
and 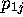 in (c)-(e) of
Proposition 2.4. Equation (i) of Proposition 2.1 now follows by choosing
j=2 and substituting (2.20) and (2.22). The equations (ii)-(iv) of
Proposition 2.1 are deduced from (c),(d) and (f) of Proposition 2.4
respectively. This requires making use of the general formula
in (c)-(e) of
Proposition 2.4. Equation (i) of Proposition 2.1 now follows by choosing
j=2 and substituting (2.20) and (2.22). The equations (ii)-(iv) of
Proposition 2.1 are deduced from (c),(d) and (f) of Proposition 2.4
respectively. This requires making use of the general formula

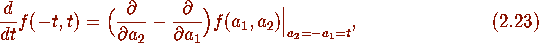 using (2.22), and noting from the first equation in Proposition 2.3 with the
substitutions (2.20) and (2.22) that
using (2.22), and noting from the first equation in Proposition 2.3 with the
substitutions (2.20) and (2.22) that

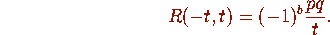 The equations (v) follow immediately from the final line of equations in
Proposition 2.3 and (2.22), and the final equation (vi) follows from
the second equation in Proposition 2.3 and (2.23).
The equations (v) follow immediately from the final line of equations in
Proposition 2.3 and (2.22), and the final equation (vi) follows from
the second equation in Proposition 2.3 and (2.23).