![[Shownotes]](../gif/annotate/sshow-61.gif)
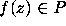 of degree 100 were computed on the Cray,
and they exhibit most of the features visible in
Figures 1,
2
and
3.
However, they are not as interesting as the lower degree zeros that are exhibited in
Figures 1,
2
and
3.
The ``spikes'' or ``tendrils'' that generate the fractal appearance in the graphs we include come from a small fraction of the
polynomials.
Sampling even
of degree 100 were computed on the Cray,
and they exhibit most of the features visible in
Figures 1,
2
and
3.
However, they are not as interesting as the lower degree zeros that are exhibited in
Figures 1,
2
and
3.
The ``spikes'' or ``tendrils'' that generate the fractal appearance in the graphs we include come from a small fraction of the
polynomials.
Sampling even 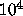 of the
of the 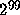 polynomials
polynomials
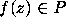 of degree 100 does not yield a good representation of the extremal features that we expect to see
for high as well as low degrees.
of degree 100 does not yield a good representation of the extremal features that we expect to see
for high as well as low degrees.
Graphs were prepared using the S system [2].
The graphs in
Figures 4,
5 and
6
were prepared differently.
A program was written that checked whether a given w with
|w| < 1 is in 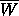 .
Note that
.
Note that

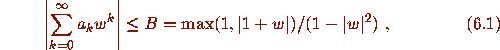 where the
where the 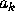 are any 0,1 coefficients,
since we can write
are any 0,1 coefficients,
since we can write

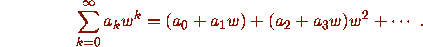 The procedure was to test all sets of 0,1 coefficients
The procedure was to test all sets of 0,1 coefficients
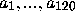 to see whether they could be the initial segment of coefficients of a power series
to see whether they could be the initial segment of coefficients of a power series

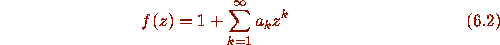 for which
for which 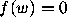 .
Let us regard the strings of coefficients
.
Let us regard the strings of coefficients 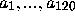 as the
leaves of a balanced binary tree, with the nodes below the root corresponding to
as the
leaves of a balanced binary tree, with the nodes below the root corresponding to
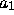 , those below to
, those below to 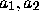 , etc.
The procedure was to explore this tree,
checking whether
, etc.
The procedure was to explore this tree,
checking whether

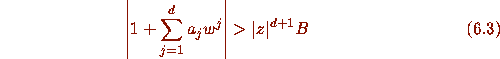 at any stage.
If
at any stage.
If 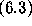 is satisfied, then w is not a zero of any power series of
the form
is satisfied, then w is not a zero of any power series of
the form 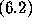 with initial coefficients
with initial coefficients
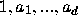 , and the subtree of that node does not have to be explored.
If all the leaves are discarded by this procedure, we have a rigorous
proof that
, and the subtree of that node does not have to be explored.
If all the leaves are discarded by this procedure, we have a rigorous
proof that 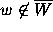 , and so in fact an open neighborhood of w is outside
, and so in fact an open neighborhood of w is outside 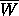 .
On the other hand, if a leaf was found with
.
On the other hand, if a leaf was found with

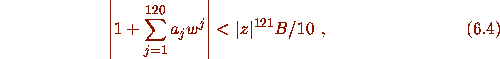 then the program assumed that
then the program assumed that 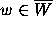 .
(By establishing lower bounds for the derivative of the polynomial
.
(By establishing lower bounds for the derivative of the polynomial
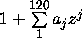 at w and using crude upper bounds for
the second derivative, one could in principle prove that there is some point
at w and using crude upper bounds for
the second derivative, one could in principle prove that there is some point  close to w such that
close to w such that 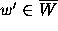 , although the 10
in condition
, although the 10
in condition 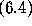 might have to be decreased.
Another way to prove this would be to use Lemma 3.1.
This step was not carried out.)
Figures 4,
5 and
6
were produced by testing each w in a
might have to be decreased.
Another way to prove this would be to use Lemma 3.1.
This step was not carried out.)
Figures 4,
5 and
6
were produced by testing each w in a 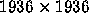 or a
or a 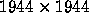 grid (corresponding to the resolution of our laser
printer).
There were few points w for which neither condition
grid (corresponding to the resolution of our laser
printer).
There were few points w for which neither condition
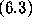 nor condition
nor condition 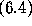 held.
The exceptions occur primarily in Fig. 4, but they do not affect
how the picture looks.
Had we used a tree of depth 80, the exceptions would have been
much more frequent.
held.
The exceptions occur primarily in Fig. 4, but they do not affect
how the picture looks.
Had we used a tree of depth 80, the exceptions would have been
much more frequent.
The computations of
Figures 4,
5 and
6
are not completely rigorous in
that the determination of 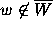 is rigorous,
while that of
is rigorous,
while that of 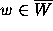 is not.
Moreover, an implicit premise in the preparation of
Figures 4,
5 and
6
was that if a point
is not.
Moreover, an implicit premise in the preparation of
Figures 4,
5 and
6
was that if a point 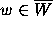 , then the whole
neighborhood of w represented by the corresponding pixel is in
, then the whole
neighborhood of w represented by the corresponding pixel is in
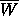 .
On the other hand, the computations of
Figures 1,
2
and
3 are
rigorous.
.
On the other hand, the computations of
Figures 1,
2
and
3 are
rigorous.
It is possible to use computations to obtain rigorous
estimates for 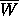 that are sharper than those of
Theorem 2.1.
As an example, we sketch how a moderate amount of straightforward computing
establishes that there are no
that are sharper than those of
Theorem 2.1.
As an example, we sketch how a moderate amount of straightforward computing
establishes that there are no 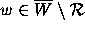 with
with 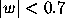 .
We modify the method of proof of Theorem 2.1.
Write
.
We modify the method of proof of Theorem 2.1.
Write

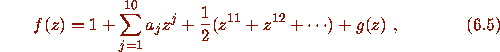 where
where

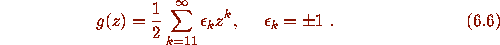 Then we can write
Then we can write

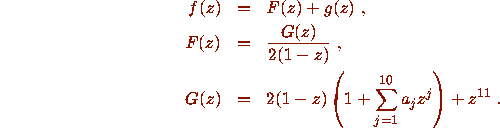 If we establish that
If we establish that 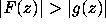 on some simple closed
contour about the origin, then by Rouché's theorem
on some simple closed
contour about the origin, then by Rouché's theorem 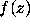 and
and 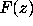 will have the same number of zeros inside that
contour.
To prove that
will have the same number of zeros inside that
contour.
To prove that 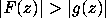 on a contour C,
it suffices to show that
on a contour C,
it suffices to show that 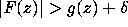 on a discrete
set of points z on C, where
on a discrete
set of points z on C, where
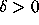 is such that bounds on the derivatives of
is such that bounds on the derivatives of 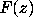 and
and 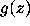 guarantee that
guarantee that 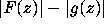 will not decrease by
more than
will not decrease by
more than 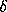 between the sampling points.
This was applied to each of the
between the sampling points.
This was applied to each of the 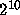 choices of
choices of
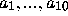 .
Of the 1024 functions
.
Of the 1024 functions 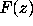 , 997 satisfied
, 997 satisfied 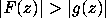 on
on

 The remaining 27 functions
The remaining 27 functions 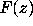 were shown to satisfy
were shown to satisfy
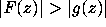 on the contour
on the contour

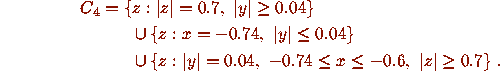 Finally, zeros of each of the 1024 polynomials
Finally, zeros of each of the 1024 polynomials 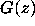 were
computed, and it was found that 85 of these polynomials had a
single zero in
were
computed, and it was found that 85 of these polynomials had a
single zero in 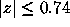 , and the remaining 939 had none.
Thus in all cases we can conclude that
, and the remaining 939 had none.
Thus in all cases we can conclude that 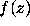 has at most one
zero in
has at most one
zero in 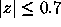 .
Such a zero has to be real.
.
Such a zero has to be real.
The estimates used above were crude, and with more care one
can either decrease the amount of computing (and even eliminate
it altogether) or obtain better bounds for 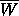 .
.
The basic principle that makes it possible to obtain good
estimates of 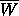 is that for extremal points
is that for extremal points 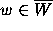 , the power series
, the power series 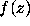 with
0,1 coefficients such that
with
0,1 coefficients such that 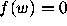 are restricted.
For example the region depicted in
Figures 3 and
4 is
are restricted.
For example the region depicted in
Figures 3 and
4 is

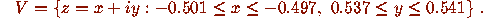 Numerical computation (evaluating polynomials of degrees
Numerical computation (evaluating polynomials of degrees 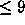 with 0,1 coefficients at a
with 0,1 coefficients at a 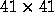 uniform grid, and
bounding derivatives) shows that if
uniform grid, and
bounding derivatives) shows that if 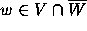 ,
then w can only be a zero of a power series of the form
,
then w can only be a zero of a power series of the form

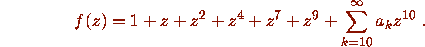 This restricted the set of
This restricted the set of 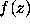 that had to be considered, and made
possible the computation of
Figure 3
, as it would not have been
feasible to examine all polynomials of degrees
that had to be considered, and made
possible the computation of
Figure 3
, as it would not have been
feasible to examine all polynomials of degrees 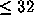 .
Furthermore, this restriction on the coefficients of
.
Furthermore, this restriction on the coefficients of 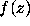 makes it possible to estimate the shape of
makes it possible to estimate the shape of 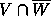 .
.
It should be possible to prove rigorously, with the help of numerical computations, such as those mentioned above, that the hole in 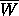 mentioned in the Introduction and pictured in
Figure 6
is isolated in the
sense that there is a continuous closed curve in
mentioned in the Introduction and pictured in
Figure 6
is isolated in the
sense that there is a continuous closed curve in 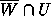 , for U a small rectangle, that encloses the hole.
We have not done this.
, for U a small rectangle, that encloses the hole.
We have not done this.
To explain the fractal appearance of 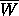 ,
suppose that
,
suppose that 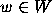 , |w| < 1, and that
, |w| < 1, and that
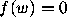 where
where

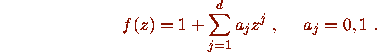 Suppose that
Suppose that

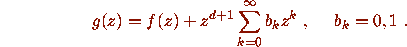 If
If 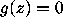 and |z-w| is small, while d is large, we have
and |z-w| is small, while d is large, we have

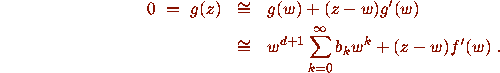 If
If 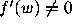 (which as far as we know may hold for all
w with |w| < 1),
then
(which as far as we know may hold for all
w with |w| < 1),
then 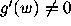 for d large enough, and we can expect
that
for d large enough, and we can expect
that

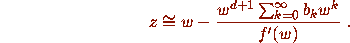 Thus if
Thus if

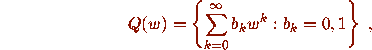 then we expect to find zeros in a neighborhood of each point of
then we expect to find zeros in a neighborhood of each point of

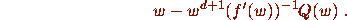 The set
The set 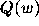 is connected [1], and for
is connected [1], and for 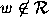 ,
it seems that it contains a small disk around the origin.
The set
,
it seems that it contains a small disk around the origin.
The set 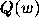 is a continuous function of w, which accounts
for the similarity of the protrusions
from
is a continuous function of w, which accounts
for the similarity of the protrusions
from 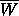 visible in
Figures 5 and
6.
(The protrusions in Fig. 4 are different,
since there the sets
visible in
Figures 5 and
6.
(The protrusions in Fig. 4 are different,
since there the sets 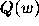 are of different shape from those in
Figures 5 and
6.)
are of different shape from those in
Figures 5 and
6.)
Acknowledgements. The authors thank E. R. Rodemich for originally raising the question of the distribution of zeros of 0,1 polynomials, M. Sambandham for providing a copy of [15], A. R. Wilks for help with graphics, and D. Zagier for informing them of the work of T. Bousch [5,6]. Special thanks are due to David desJardins and Emanuel Knill for permission to use their proofs of Lemma 5.1.