In[20]:=
The intersection points correspond to equilibria, and we now know how to find them efficiently. But what of all the different regions? A moment's thought will convince you that within each region the compass direction of the underlying vector field is one of NE, NW, SE, or SW. Thus these regions can be a valuable tool in understanding and illustrating the orbit behavior.In[21]:=
Out[21]Certainly the image becomes much more informative when we superimpose some orbits. We show how to do that using NDSolve (the full VisualDSolve package allows a one-line treatment of such combined images).
In[22]:=
From now on we will generally suppress the Mathematica code. The
preceding example should provide enough information for the reader to generate
these as will as his or her own examples.
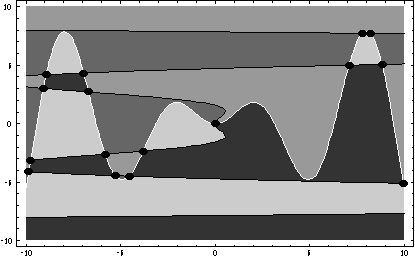
The next image shows the gray regions for our main example, followed by an
image of the orbits. The shaded regions allow for a quicker and better
interpretation of the orbit structure. The NullclineStyle option is used to
distinguish the x-nullclines (black) from the y-nullclines (white).
In[23]:=
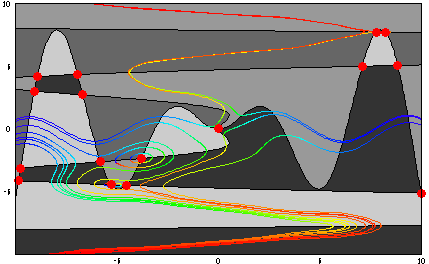
Here is a view of some orbits, colored to represent increasing t (from red to blue).
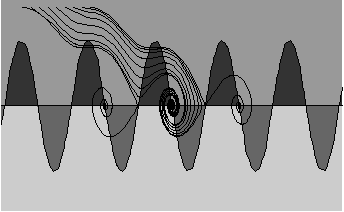
And here is an image of the CODEE teddy bears (cover of the Spring 1995 CODEE newsletter; also [BCB, p. 304]). This example shows that the algorithm is capable of dealing with a very complicated contour plot. This takes a bit of time (and memory) even on a fast computer! We are rewarded with a detailed view of the bear's phase plane and an unexpected glimpse of a latent bear: the contours at the bottom of the image form a bear's head!
In[24]:=
Out[24]
Getting the shaded regions was not easy. Here is a bare outline of our
algorithm. The main idea is to take the all the curves in the nullcline data
produced by the contour plots and subdivide them at certain "critical"
x-values. An x-value is critical if it is
* one of the x-bounds of the rectangle;
* the x-coordinate of a point at which a curve stops going left and starts
going right, or vice
versa (i.e., a division point that refines the curve data into graphs of
functions);
* the x-coordinate of an equilibrium point;
* the x-coordinate of a point where a contour leaves the rectangle at the top
or the bottom;
* the x-coordinate of the first or last point in one of the contour data
segments (e.g., a contour that is a closed curve has to start somewhere; that
starting x-value will be critical).
Once all the contour data is partitioned so that each curve occupies a strip
between consecutive critical x-values -- thus defining a function of x and not
intersecting any other curve -- we are in good shape. For each piece of curve we
can form the polygon whose bottom border is the curve and whose left and right
sides run vertically all the way to the top. The idea is then to color these
polygons appropriately; if they are sorted properly then, when one overlays
another, its gray will paint over the gray of the one underneath. To sort, and
to determine which shade of gray to use, we go to the center of the x-domain
(the average of two adjacent critical x-values), and look at where the vertical
line at this point intersects all the curves; we use this information to do our
sorting, and we take the average of successive intersection points to get
interior points at which to evalute f and g and so determine a gray shade. Whew!
This is horrendously complicated! But it works well and because the data sets
are not too large, it runs fairly quickly.
Note that the final images are a bit of an optical illusion. The first example,
the pendulum, looks like 14 shaded polygons. But in reality there are 36
polygons, because the many strips formed by the critical x-values mean that the
large polygons are made up of several smaller ones. The bear example, which
visually appears as a gorup of about 100 polygons, actually consists of 921
smaller polygons.
Exercise. If the user wishes to shade in the regions where a field points N, S,
E, and W (instead of NW, SW, NE, SE), that is possible via NullclinePlot[{f - g,
f + g}, ***]. The equilibrium points will be visible in the same way.
There are several options to NullclinePlot (defaults in parentheses):
NullclineShading turns the shading on or off (False).
Nullclines sets whether the curves forming the nullclines are shown
(True).
NullclineContourPlotPoints controls the resolutiuon of the contour
plots that get everything started (20).
ShowEquilibria causes a point to appear at each equilibrium point (False); its
color is
controlled by EquilibriumPointColor (RGBColor[0, 0, 0]).
NullclineShadingMethod causes the underlying algorithm to switch to the
density plot
method alluded to earlier. This is useful for the occasional example for which
the
primary method fails (see the example based on the Dirac delta function in
section 3).
NullclineStyle allows the user to set distinct styles for the x- and
y-nullclines ({{}, {}}).