A troublesome case: the Dirac delta function

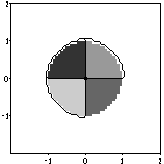
The shading algorithm is by no means infallible. For example, it needs a discrete set of equilibrium points in order to proceed, while some functions have an overabundance of critical points. The following example is based on a step function and every point on or outside the unit disk is an equilibrium point! To deal with these cases we have included a switch that calls upon the alternative method alluded to earlier: a density plot of the sum of signs. Setting the NullclineShadingMethod to SumOfSigns forces the alternative method to be used. The results for this troublesome example are not ideal, but they are roughly accurate, with a white region showing the region of equilibrium points outside the unit disk.

In[26]:=


If your output will be a sequence of graphs, select a display option.
Display as:

Up to 3. More Examples