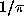including
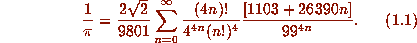This series adds roughly eight digits per term and was used by Gosper in
1985 to compute 17 million terms of the continued fraction for 
. Such
series exist because various modular invariants are rational (which is
more-or-less equivalent to identifying those imaginary quadratic fields
with class number 1) see [3]. The larger the discriminant of such a field
the greater the rate of convergence. Thus with d = -163 we have the
largest of the class number 1 examples
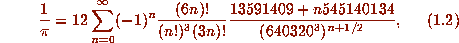a series first displayed by the Chudnovskys [10]. The underlying approximation
also produces 
and is correct to 16 places.
Quadratic versions of these series correspond to class number two imaginary quadratic fields. The most spectacular and largest example has d = -427 and
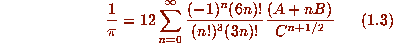where
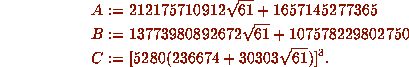This series adds roughly twenty-five digits per term, 
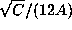already agrees with pi to twenty-five places [3]. The last
two series are of the form
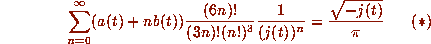where
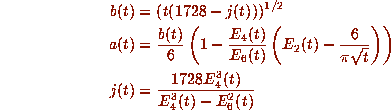Here t is the appropriate discriminant, j is the ``absolute
invariant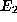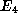'', and 
, 
and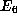 
are Eisenstein series.
For a further discussion of these see [2] where many such quadratic
examples are considered. Various of the recent record setting calculations
of pi have been based on these series. In particular the Chudnovskys
computed over two billion digits of 
using the second series above.
There is an unlimited number of such series with increasingly more rapid
convergence. The price one pays is that one must deal with more
complicated algebraic irrationalities. Thus a class number p field will
involve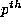 
degree algebraic integers as the constants 
, 
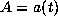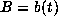and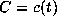 
in the series. The largest class number three example
of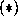 
corresponds to d = -907 and gives 37 or 38 digits per
term. It is
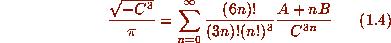where
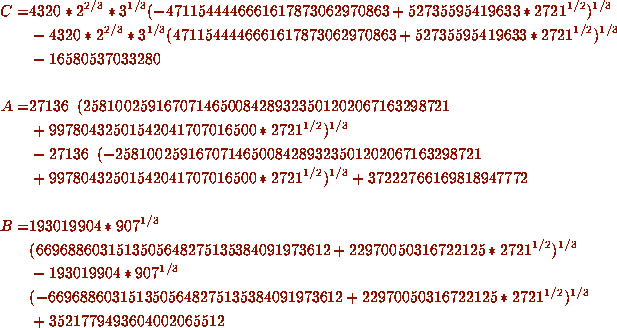The series we computed of largest discriminant was the class number four
example with d = -1555. Then
The series (1.4) with these constants gives 50 additional digits per
term.
The Computational Component. The absolute invariant,
and so the coefficients A, B, and C satisfy polynomial equations of
known degree and height. Thus the problem of determining the coefficients
of each series reduces to algebra and can be entirely automated. This is
really the dream case for computer aided analysis. Indeed from the
expressions for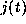 
, 
, 
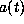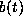we straightforwardly computed their
values to several hundred digits. The lattice basis reduction algorithm, as
implemented in Maple, now provides the minimal polynomials for each
quantity. In addition, a higher precision calculation actually provides a
proof of the claimed identity. This last step requires knowing a priori
bounds on the degrees and heights of the invariants. While somewhat
mathematically sophisticated, the computation required is fairly easy
though a little slow.
![[Annotate]](/organics/icons/sannotate.gif){kind=icon}
![[Shownotes]](../gif/annotate/sshow-31.gif)