Contents Next: The Markov Process Up: No Title Previous: No Title

Introduction

The now-famous card trick known as ``Kruskal's Principle'', or the ``Kruskal Count'' among professional card magicians, originated with the physicist Kruskal, of Princeton University [see 2, p. 274]. The trick runs as follows. The dealer asks the player to silently pick a number from 1 to 10, call it

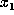. This number becomes the player's first ``secret'' card. From this point onward, there is no more communication between the dealer and the player. The dealer now begins dealing cards, face up, and when the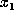

'th card comes up, its face value, say

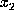, determines that the next ``secret'' card is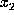

cards further into the deck. The player keeps track of his new secret cards

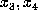, etc. The dealer continues to deal cards, and at some point stops to announce that she has magically reached one of the player's secret cards.

How does the trick work? Well, the dealer picks her own secret card to begin the process in her mind, say 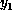. She now carries out the same procedure, keeping track of her secret cards 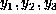, etc. She keeps dealing for a while and then points out one of her own secret cards. Probabilistically, her sequence and the player's sequence will dove tail into the same sequence. The main point is that as soon as one of her secret cards coincides with one of the player's secret cards, their two sequences of secret cards are identical from that point onward.

A natural question is: ``what is the probability that the dealer will correctly guess one of the player's secret cards after n cards have been dealt?'' We reduce the problem to a discrete, absorbing Markov Process. In general, we find the m by m matrix of transition probabilites for a ``deck'' of cards with m face values. In the last section we go back to the standard deck with m=10 face values, where we throw out the jacks, queens, and kings for simplicity.

The authors would like to thank Jeff Lagarias for pointing out an interesting preprint [4] which uses somewhat different methods. Martin Gardner has also discussed this card trick in his column of the Scientific American [3].

Contents Next: The Markov Process Up: No Title Previous: No Title