![[Shownotes]](../gif/annotate/sshow-11.gif)
There are writings on the wall that, now that the silicon savior has arrived, a new testament is going to be written. Although there will always be a small group of ``rigorous'' old-style mathematicians(e.g. [JQ]) who will insist that the true religion is theirs, and that the computer is a false Messiah, they may be viewed by future mainstream mathematicians as a fringe sect of harmless eccentrics, like mathematical physicists are viewed by regular physicists today.
The computer has already started doing to mathematics what the
telescope and microscope did to astronomy and biology.
In the future, not all mathematicians will care about absolute certainty,
since there will be so many exciting new facts to discover: mathematical
pulsars and quasars that will make the Mandelbrot set seem like a mere
Jovian moon. We will have (both human and machine![]() For example, my computer Shalosh B. Ekhad,
and its friend Sol Tre, already have a
non-trivial publication list, e.g. [E], [ET]
) professional theoretical mathematicians, who will
develop conceptual paradigms to make sense out of the empirical data,
and who will reap Fields medals along with (human and machine)
experimental mathematicians. Will there still be a place for
mathematical mathematicians?
This will happen after a transitory age of semi-rigorous mathematics,
in which identities (and perhaps other kinds of theorems) will carry
price-tags.
For example, my computer Shalosh B. Ekhad,
and its friend Sol Tre, already have a
non-trivial publication list, e.g. [E], [ET]
) professional theoretical mathematicians, who will
develop conceptual paradigms to make sense out of the empirical data,
and who will reap Fields medals along with (human and machine)
experimental mathematicians. Will there still be a place for
mathematical mathematicians?
This will happen after a transitory age of semi-rigorous mathematics,
in which identities (and perhaps other kinds of theorems) will carry
price-tags.
A Taste Of Things To Come
To get a glimpse of how mathematics will be practiced in the not too far future, I will describe the case of algorithmic proof theory for hypergeometric identities[WZ*][Z*][Ca]. In this theory, it is possible to rigorously prove, or refute, any conjectured identity belonging to a wide class of identities, that includes most of the identities between the classical special functions of mathematical physics. Any such identity is proved by exhibiting a proof certificate, that reduces the proof of the given identity to that of a finite identity among rational functions, and hence, by clearing denominators, to that between specific polynomials.
This algorithm can be performed successfully on all ``natural identities'' we are now aware of. It is easy, however, to concoct artificial examples for which the running time, and memory, are prohibitive. Undoubtedly, in the future ``natural'' identities will be encountered whose complete proof will turn out to be not worth the money. We will see later, how, in such cases, one can get ``almost certainty'' with a tiny fraction of the price, along with the assurance that if we robbed a bank, we would be able to know for sure.
This is vaguely reminiscent of transparent proofs introduced
recently in theoretical computer science[Ci][ALMSS][AS].
The result that there exist short theorems
having arbitrarily long proofs, a consequence of Gödel's incompleteness
theorem, also comes to mind [S].![]() Namely, the ratio (proof length)/(theorem length) grows fast
enough to be non-recursive.
Adding an axiom can shorten proofs by recursive amounts [G], [D].
I speculate that similar developments
will occur elsewhere in mathematics, and will ``trivialize'' large
parts of mathematics, by reducing mathematical truths to routine,
albeit possibly very long, and exorbitantly expensive to check,
``proof certificates''. These proof certificates would also
enable us, by plugging in random values,
to assert ``probable truth'' very cheaply.
Namely, the ratio (proof length)/(theorem length) grows fast
enough to be non-recursive.
Adding an axiom can shorten proofs by recursive amounts [G], [D].
I speculate that similar developments
will occur elsewhere in mathematics, and will ``trivialize'' large
parts of mathematics, by reducing mathematical truths to routine,
albeit possibly very long, and exorbitantly expensive to check,
``proof certificates''. These proof certificates would also
enable us, by plugging in random values,
to assert ``probable truth'' very cheaply.
Identities
Many mathematical theorems are identities: statements of type ``='', which take the form A=B. Here is a sampler, in roughly an increasing order of sophistication.
1. 2+2=4.

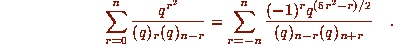

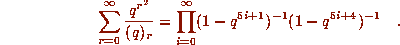

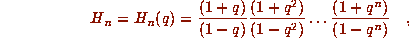
then

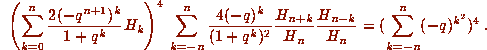
8'.

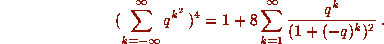
9. Analytic Index=Topological Index.
10. 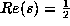 for every
non-real s such that
for every
non-real s such that  .
.
All the above identities are trivial, except possibly the last two, which I think quite likely will be considered trivial in two hundred years. I will now explain.
Why are the first 8 identities trivial?
The first identity, while trivial nowadays, was very deep when it was first discovered, independently, by several anonymous cave-dwellers. It is a general, abstract theorem, that contains, as special cases, many apparently unrelated theorems: Two bears and Two bears make Four bears, Two apples and Two apples make Four apples, etc. It was also realized that in order to prove it rigorously, it suffices to prove it for any one special case, say, marks on the cave's wall.
The second identity: 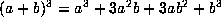 , is of one
level of generality higher. Taken literally (in the semantic sense
of the word literally), it is a fact about numbers. For any
specialization of a and b we get yet another correct numerical
fact, and as such it requires a ``proof'', invoking the commutative,
distributive and associative ``laws''. However,
it is completely routine when viewed literally,
in the syntactic sense, i.e. in which a and b are no longer
symbols denoting numbers, but rather represent themselves,
qua (commuting) literals.
This shift in emphasis roughly corresponds to the transition from
Fortran to Maple, i.e. from numeric computation to
symbolic computation.
Identities 3 and 4 can be easily embedded in classes of routinely
verifiable identities in several ways. One way is by
defining
, is of one
level of generality higher. Taken literally (in the semantic sense
of the word literally), it is a fact about numbers. For any
specialization of a and b we get yet another correct numerical
fact, and as such it requires a ``proof'', invoking the commutative,
distributive and associative ``laws''. However,
it is completely routine when viewed literally,
in the syntactic sense, i.e. in which a and b are no longer
symbols denoting numbers, but rather represent themselves,
qua (commuting) literals.
This shift in emphasis roughly corresponds to the transition from
Fortran to Maple, i.e. from numeric computation to
symbolic computation.
Identities 3 and 4 can be easily embedded in classes of routinely
verifiable identities in several ways. One way is by
defining 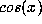 and
and 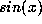 by
by 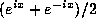 and
and 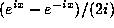 , and the
Fibonacci numbers
, and the
Fibonacci numbers 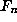 by Binet's formula.
by Binet's formula.
Identities 5-8 were, until recently, considered genuine non-trivial
identities, requiring a human demonstration. One particularly nice
human proof of 6, was given by Cartier and Foata[CF].
A one-line computer-generated proof of identity 6 is given in
[E]. Identities 7 and 8
are examples of so-called q-binomial coefficient
identities, (a.k.a. terminating q-hypergeometric series.)
All such identities are now routinely provable[WZ2](see below.)
The machine-generated proofs of 7 and 8 appear in
[ET] and [AEZ] respectively. Identities
7 and 8 immediately imply,
by taking the limit  ,
identities 7' and 8', which, in turn, are equivalent to two famous
number-theoretic statements: The first Rogers-Ramanujan identity,
that asserts that the number of partitions of an integer into parts
that leave remainder 1 or 4 when divided by 5 equals
the number of partitions of that integer into parts that differ
from each other by at least 2, and Jacobi's
theorem that asserts that
the number of representations of an integer as a sum of
4 squares, equals 8 times the sum of its divisors that
are not multiples of 4.
,
identities 7' and 8', which, in turn, are equivalent to two famous
number-theoretic statements: The first Rogers-Ramanujan identity,
that asserts that the number of partitions of an integer into parts
that leave remainder 1 or 4 when divided by 5 equals
the number of partitions of that integer into parts that differ
from each other by at least 2, and Jacobi's
theorem that asserts that
the number of representations of an integer as a sum of
4 squares, equals 8 times the sum of its divisors that
are not multiples of 4.
The WZ Proof Theory
Identities 5-8 involve sums of the form


where the summand, 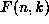 , is a
hypergeometric term, (in 5, and 6), or a
q-hypergeometric term, (in 7, and 8),
in both n and k, which means
that both quotients
, is a
hypergeometric term, (in 5, and 6), or a
q-hypergeometric term, (in 7, and 8),
in both n and k, which means
that both quotients 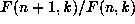 and
and 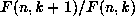 are
rational functions of
are
rational functions of 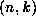 (
(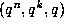 respectively).
respectively).
For such sums, and multi-sums, we have ([WZ2]) the following result.
The Fundamental Theorem of Algorithmic Hypergeometric Proof Theory:
Let 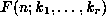 be a proper (see [WZ2])
hypergeometric term in
all of
be a proper (see [WZ2])
hypergeometric term in
all of 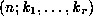 .
Then there exist polynomials
.
Then there exist polynomials
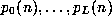 and rational functions
and rational functions
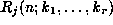 such that
such that 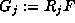 satisfy
satisfy

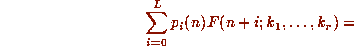

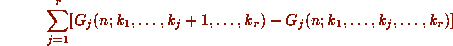
and hence, if for every specific n, 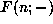 has compact support in
has compact support in
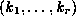 , the definite sum,
, the definite sum, 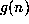 , given by
, given by

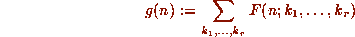
satisfies the linear recurrence equation with polynomial coefficients:


 follows from
follows from  by summing over
by summing over
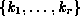 , and observing that all the sums
on the right telescope to zero.
, and observing that all the sums
on the right telescope to zero.
If the recurrence happens to be first order, i.e. L=1 above,
then it can be written in closed form: for example the solution
of the recurrence 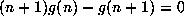 ,
, 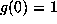 , is
, is 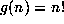 .
.
This ``existence'' theorem also implies an algorithm for finding
the recurrence (i.e. the 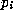 ) and the accompanying certificates
) and the accompanying certificates
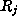 , see below.
, see below.
An analogous theorem holds for q-hypergeometric series[WZ2][K].
Since we know how to find, and prove, the recurrence satisfied by any given hypergeometric sum or multi-sum, we have an effective way of proving any equality of two such sums, or the equality of a sum with a conjectured sequence. All we have to do is check whether both sides are solutions of the same recurrence, and match the appropriate number of initial values. Furthermore, we can also use the algorithm to find new identities. If a given sum yields a first-order recurrence, it can be solved, as mentioned above, and the sum in question turns out to be explicitly evaluable. If the recurrence obtained is of higher order, then most likely the sum is not explicitly-evaluable (in closed form), and Petkovsek's algorithm[P], that decides whether a given linear recurrence (with polynomial coefficients) has closed form solutions, can be used to find out for sure.
Almost Certainty For An  Of The Cost
Of The Cost
Consider identity 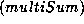 once again, where
once again, where 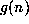 is ``nice''.
Dividing through by
is ``nice''.
Dividing through by 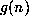 and letting
and letting 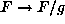 (Herb Wilf's
wonderful trick), we can assume that we have to prove an identity of
the form
(Herb Wilf's
wonderful trick), we can assume that we have to prove an identity of
the form


The WZ theory promises you that the left side satisfies some
linear recurrence, and if the identity is indeed true, then the
sequence 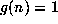 should be a solution (in other words
should be a solution (in other words
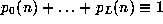 ). For the sake of
simplicity, let's assume that the recurrence is minimal,
i.e. is
). For the sake of
simplicity, let's assume that the recurrence is minimal,
i.e. is 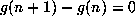 ,
(this is true anyway in the vast majority of the cases.)
To prove the identity, by this method, we have to find rational functions
,
(this is true anyway in the vast majority of the cases.)
To prove the identity, by this method, we have to find rational functions
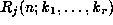 such that the
such that the 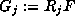 satisfy:
satisfy:

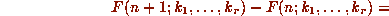

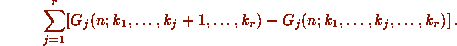
By dividing 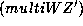 through by F, and clearing denominators,
we get a certain functional equation for the
through by F, and clearing denominators,
we get a certain functional equation for the 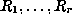 ,
from which it is possible to determine their denominators
,
from which it is possible to determine their denominators
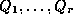 . Writing
. Writing 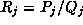 , the proof boils down
to finding polynomials
, the proof boils down
to finding polynomials 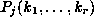 , with
coefficients that are rational functions in n and possibly
other (auxiliary) parameters. It is easy to predict upper
bounds for the degrees of the
, with
coefficients that are rational functions in n and possibly
other (auxiliary) parameters. It is easy to predict upper
bounds for the degrees of the 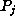 in
in 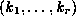 .
We then express each
.
We then express each 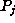 symbolically, with ``undetermined''
coefficients, and substitute into the above-mentioned functional equation.
We then expand,
and equate coefficients of all monomials
symbolically, with ``undetermined''
coefficients, and substitute into the above-mentioned functional equation.
We then expand,
and equate coefficients of all monomials 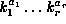 ,
and get an (often huge) system of inhomogeneous linear
equations with symbolic coefficients. The proof boils
down to proving that this inhomogeneous system of linear
equations has a solution. It is very time-consuming to solve
a system of linear equations with symbolic coefficients.
By plugging in
specific values for n and the other parameters, if present,
one gets a system with numerical coefficients, which is much
faster to handle. Since it is unlikely that a random system of
inhomogeneous linear
equations with more equations than unknowns can be solved,
the solvability of the system for a number of special values of
n and the other parameters
is a very good indication that the identity is indeed true.
It is a waste of money to get absolute certainty,
unless the conjectured identity in question is known
to imply the Riemann Hypothesis.
,
and get an (often huge) system of inhomogeneous linear
equations with symbolic coefficients. The proof boils
down to proving that this inhomogeneous system of linear
equations has a solution. It is very time-consuming to solve
a system of linear equations with symbolic coefficients.
By plugging in
specific values for n and the other parameters, if present,
one gets a system with numerical coefficients, which is much
faster to handle. Since it is unlikely that a random system of
inhomogeneous linear
equations with more equations than unknowns can be solved,
the solvability of the system for a number of special values of
n and the other parameters
is a very good indication that the identity is indeed true.
It is a waste of money to get absolute certainty,
unless the conjectured identity in question is known
to imply the Riemann Hypothesis.
Semi-Rigorous Mathematics
As wider classes of identities, and perhaps even other kinds of
classes of theorems, become routinely-provable, we might witness
many results for which we would know how to find a proof (or refutation),
but we would be unable, or unwilling, to pay for finding such proofs,
since ``almost certainty'' can be bought so much cheaper. I can envision
an abstract of a paper, c. 2100, that reads :
``We show, in a certain precise sense,
that the Goldbach conjecture is true with probability larger than 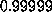 ,
and that its complete truth could be determined with a budget of
,
and that its complete truth could be determined with a budget of
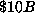 .''
It would be then OK to rely on such a priced theorem, provided that
the price is stated explicitly. Whenever statement A, whose price is
p, and statement B, whose price is q, are used to deduce statement C,
the latter becomes a priced theorem priced at p+q.
.''
It would be then OK to rely on such a priced theorem, provided that
the price is stated explicitly. Whenever statement A, whose price is
p, and statement B, whose price is q, are used to deduce statement C,
the latter becomes a priced theorem priced at p+q.
If a whole chain of boring identities would turn out to imply an interesting one, we might be tempted to redeem all these intermediate identities, but we would not be able to buy out the whole store, and most identities would have to stay unclaimed.
As absolute truth becomes more and more expensive, we would sooner or later come to grips with the fact that few non-trivial results could be known with old-fashioned certainty. Most likely we will wind up abandoning the task of keeping track of price altogether, and complete the metamorphosis to non-rigorous mathematics. Note: Maple programs for proving hypergeometric identities are available by anonymous ftp to math.temple.edu, in directory pub/zeilberger/programs. a Mathematica implementation of the single-summation program, can be obtained from Peter Paule at paule@risc.uni-linz.ac.at .
References
[AZ] G. Almkvist and D. Zeilberger, The method of differentiating under the integral sign, J. Symbolic Computation 10(1990), 571-591.
[AEZ] G. E. Andrews, S. B. Ekhad, and D. Zeilberger A short proof of Jacobi's formula for the number of representations of an integer as a sum of four squares, Amer. Math. Monthly, 100(1993), 274-276.
[ALMSS] S. Arora, C. Lund, R. Motwani, M. Sudan, and M. Szegedy, Proof verification and intractability of approximation problems, Proc. 33rd Symp. on Foundations of Computer Science (FOCS), IEEE Computer Science Press, Los Alamitos, 1992, pp. 14-23.
[AS] S. Arora, and M. Safra, Probabilstic checking of proofs, ibid, pp. 2-13.
[Ca] P. Cartier, Démonstration ``automatique'' d'identités et
fonctions hypergéometriques [d'apres D. Zeilberger], Séminaire
Bourbaki, exposé  746, Astérisque 206, 41-91, SMF, 1992.
746, Astérisque 206, 41-91, SMF, 1992.
[CF] P. Cartier and D. Foata, Problèmes combinatoires de commutation et réarrangements, Lecture Notes Math. v. 85, Springer 1969.
[Ci] B. Cipra, Theoretical computer scientists develop transparent proof techniques, SIAM News, 25/3(May 1992).
[D] J. Dawson, The Gödel incompleteness theorem from a length of proof perspective, Amer. Math. Monthly 86(1979), 740-747.
[E] S. B. Ekhad, A very short proof of Dixon's theorem, J. Comb. Theo. Ser. A 54(1990), 141-142.
[ET] S. B. Ekhad and S. Tre, A purely verification proof of the first Rogers-Ramanujan identity, J. Comb. The. Ser. A 54(1990), 309-311.
[G] K. Gödel, On length of proofs, (in German) Ergeb. Math. Colloq. 7(1936), 23-24. Translated in ``The Undecidable'' (M. Davis, Ed.), Raven Press, Hewitt, NY, 1965, 82-83.
[JQ] A. Jaffe and F. Quinn, ``Theoretical mathematics'': Toward a cultural synthesis of mathematics and theoretical physics, Bulletin(N.S.) of the Amer. Math. Soc. 29(1993), 1-13.
[K] T. H. Koornwinder, Zeilberger's algorithm and its q-analogue, University of Amsterdam Mathematics department preprint.
[P] M. Petkovsek, Hypergeometric solutions of linear recurrence equations with polynomial coefficients, J. Symbolic Computation 14(1992), 243-264.
[S] J. Spencer, Short theorems with long proofs, Amer. Math. Monthly 90(1983), 365-366.
[WZ1] H. S. Wilf and D. Zeilberger, Rational functions certify combinatorial identities, J. Amer. Math. Soc. 3(1990), 147-158.
[WZ1a] ------, Towards computerized proofs of identities, Bulletin(N.S.) of the Amer. Math. Soc. 23(1990), 77-83.
[WZ2] -------, An algorithmic proof theory for hypergeometric (ordinary and ``q'') multisum/integral identities, Invent. Math. 108(1992), 575-633.
[WZ2a] ------, Rational function certification of hypergeometric multi-integral/sum/``q'' identities, Bulletin(N.S.) of the Amer. Math. Soc. 27(1992) 148-153.
[Z1] D. Zeilberger, A Holonomic systems approach to special functions identities, J. of Computational and Applied Math. 32(1990), 321-368.
[Z2]------, A Fast Algorithm for proving terminating hypergeometric identities, Discrete Math 80(1990), 207-211.
[Z3]------, The method of creative telescoping, J. Symbolic Computation 11(1991), 195-204.
[Z4]------, Closed Form (pun intended!), ``Special volume in memory of Emil Grosswald'', M. Knopp and M. Sheingorn, eds., Contemporary Mathematics 143, 579-607, AMS, Providence, 1993.
July 1993 ; Revised: August 1993.