In 1987, Chen Zhijie studied a particular irreducible 16-dimensional
module V for the general linear group 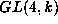 over an
algebraically closed field k of characteristic 3. Chen's interest
in this module stemmed from the analysis of prehomogeneous vector
spaces in prime characteristic. These are representations which have
a dense orbit in the underlying vector space (considered as an affine
variety). Such representations were studied extensively in
characteristic 0 in [SK]. Chen showed that V is a prehomogeneous
vector space for
over an
algebraically closed field k of characteristic 3. Chen's interest
in this module stemmed from the analysis of prehomogeneous vector
spaces in prime characteristic. These are representations which have
a dense orbit in the underlying vector space (considered as an affine
variety). Such representations were studied extensively in
characteristic 0 in [SK]. Chen showed that V is a prehomogeneous
vector space for 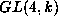 which has a relative invariant (cf. [Z])
of degree 8. The set of vectors at which this invariant takes a
nonzero value is the dense orbit.
Having a dense orbit in V is a necessary condition for a linear
algebraic group over an algebraically closed field
(such as
which has a relative invariant (cf. [Z])
of degree 8. The set of vectors at which this invariant takes a
nonzero value is the dense orbit.
Having a dense orbit in V is a necessary condition for a linear
algebraic group over an algebraically closed field
(such as 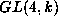 ) to have finitely many orbits in V.
) to have finitely many orbits in V.
 Annotation Form Interface
Annotation Form Interface
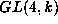 over an
algebraically closed field k of characteristic 3. Chen's interest
in this module stemmed from the analysis of prehomogeneous vector
spaces in prime characteristic. These are representations which have
a dense orbit in the underlying vector space (considered as an affine
variety). Such representations were studied extensively in
characteristic 0 in [SK]. Chen showed that V is a prehomogeneous
vector space for
over an
algebraically closed field k of characteristic 3. Chen's interest
in this module stemmed from the analysis of prehomogeneous vector
spaces in prime characteristic. These are representations which have
a dense orbit in the underlying vector space (considered as an affine
variety). Such representations were studied extensively in
characteristic 0 in [SK]. Chen showed that V is a prehomogeneous
vector space for 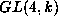 which has a relative invariant (cf. [Z])
of degree 8. The set of vectors at which this invariant takes a
nonzero value is the dense orbit.
Having a dense orbit in V is a necessary condition for a linear
algebraic group over an algebraically closed field
(such as
which has a relative invariant (cf. [Z])
of degree 8. The set of vectors at which this invariant takes a
nonzero value is the dense orbit.
Having a dense orbit in V is a necessary condition for a linear
algebraic group over an algebraically closed field
(such as 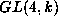 ) to have finitely many orbits in V.
) to have finitely many orbits in V.