![[Shownotes]](../gif/annotate/shide-11.gif)
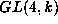 over an
algebraically closed field k of characteristic 3. Chen's interest
in this module stemmed from the analysis of prehomogeneous vector
spaces in prime characteristic. These are representations which have
a dense orbit in the underlying vector space (considered as an affine
variety). Such representations were studied extensively in
characteristic 0 in [SK]. Chen showed that V is a prehomogeneous
vector space for
over an
algebraically closed field k of characteristic 3. Chen's interest
in this module stemmed from the analysis of prehomogeneous vector
spaces in prime characteristic. These are representations which have
a dense orbit in the underlying vector space (considered as an affine
variety). Such representations were studied extensively in
characteristic 0 in [SK]. Chen showed that V is a prehomogeneous
vector space for 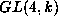 which has a relative invariant (cf. [Z])
of degree 8. The set of vectors at which this invariant takes a
nonzero value is the dense orbit.
Having a dense orbit in V is a necessary condition for a linear
algebraic group over an algebraically closed field
(such as
which has a relative invariant (cf. [Z])
of degree 8. The set of vectors at which this invariant takes a
nonzero value is the dense orbit.
Having a dense orbit in V is a necessary condition for a linear
algebraic group over an algebraically closed field
(such as 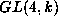 ) to have finitely many orbits in V.
) to have finitely many orbits in V.
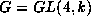 . The
20-dimensional kG-module
. The
20-dimensional kG-module
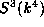 of all homogeneous polynomials of degree 3 on
of all homogeneous polynomials of degree 3 on 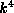 has a 4-dimensional submodule consisting of all
cubes of linear forms on
has a 4-dimensional submodule consisting of all
cubes of linear forms on 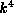 .
Modding out this submodule leads to
the 16-dimensional irreducible kG-module V studied by Chen Zhijie.
Thus
.
Modding out this submodule leads to
the 16-dimensional irreducible kG-module V studied by Chen Zhijie.
Thus
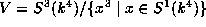 .
.
In [Z], Chen Zhijie produced eight G-orbits of nonzero vectors in V (one of which is dense) and conjectured there are no others. In this paper we find two more (of dimensions 12 and 14) and show that these are all.
Theorem.
There are exactly ten G-orbits of vectors in 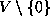 .
Representative vectors for these orbits are listed in Table 1.
.
Representative vectors for these orbits are listed in Table 1.
Our proof uses Chen's techniques, but has three additional features.
First, we use comparison with the finite field case so as to conclude
that there are no further orbits of dimension 14. This part of the
proof, including a full description of orbits in the case where k is
finite, is given in . Second, we deploy Lie algebras to find the
vector stabilizers in an efficient way. Third, and perhaps most
crucial, we use computer algebra to automate the computations
involved. In particular, the computer computations of the image of a
given vector under a given group element, of the dimension of the
space of images of a vector under the algebra of all
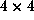 -matrices over k, and of the full stabilizer of a given
vector have been of great use. We have double checked these
computations, by having one author perform the calculations in Maple,
and the other (independently) in Mathematica. One purpose of these
computations is to find an algorithm for transforming any vector in an
orbit of dimension 13 or less into its representative in Table 1.
This part of the proof is given in .
-matrices over k, and of the full stabilizer of a given
vector have been of great use. We have double checked these
computations, by having one author perform the calculations in Maple,
and the other (independently) in Mathematica. One purpose of these
computations is to find an algorithm for transforming any vector in an
orbit of dimension 13 or less into its representative in Table 1.
This part of the proof is given in .
In a lecture at the AMS/LMS meeting in July 1992, Martin Liebeck
mentioned the above G-module V as one of the open cases in a
prospective classification of irreducible modules for almost simple
algebraic groups over an algebraically closed field of positive
characteristic for which there are a finite number of orbits on
points. This classification problem extends work of Kac, Popov
and Vinberg in characteristic 0 (cf. [KPV]) to arbitrary
characteristic. We are
grateful to R. Guralnick for showing us a preliminary version of the
preprint [GLMS] and for help with other parts of the paper particularly
section 6. Apart from the examples that also arise in
characteristic 0, a short list of examples typical for certain
positive characteristics appears in [GLMS]. The above
pair 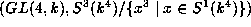 is among them.
For most examples, [GLMS]
contains a proof that the groups have finitely many orbits in these
modules indeed, but for our particular example, it
refers to the present paper for a proof. The search may be put
in the wider context of finding all pairs of subgroups in almost
simple algebraic groups over algebraically closed fields for
which there are only finitely many double cosets. For
our case in
is among them.
For most examples, [GLMS]
contains a proof that the groups have finitely many orbits in these
modules indeed, but for our particular example, it
refers to the present paper for a proof. The search may be put
in the wider context of finding all pairs of subgroups in almost
simple algebraic groups over algebraically closed fields for
which there are only finitely many double cosets. For
our case in 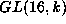 there are finitely many double cosets
over the subgroups
there are finitely many double cosets
over the subgroups 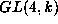 and the stabilizer of a point
in the 16 dimensional vector space. This is an example where
one subgroup is parabolic and the other subgroup is not contained in
a parabolic and so acts irreducibly.
and the stabilizer of a point
in the 16 dimensional vector space. This is an example where
one subgroup is parabolic and the other subgroup is not contained in
a parabolic and so acts irreducibly.
To finish this introduction, we would like to note that the
relative invariant of degree 8 does not seem to be as exceptional as
one might think.
For, if 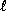 is a field of arbitrary characteristic distinct from 2,
there still is a nonzero relative invariant of degree 8 on
the 20-dimensional irreducible module
is a field of arbitrary characteristic distinct from 2,
there still is a nonzero relative invariant of degree 8 on
the 20-dimensional irreducible module 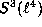 ,
as has been noted by Salmon (cf. [S]) and
verified by a straightforward computation using LiE
(cf. [LiE]). Since the projective space of the module can be viewed
as the variety of all cubic surfaces in projective space, we
would be interested in an explanation for the existence of the
relative invariant in this context.
,
as has been noted by Salmon (cf. [S]) and
verified by a straightforward computation using LiE
(cf. [LiE]). Since the projective space of the module can be viewed
as the variety of all cubic surfaces in projective space, we
would be interested in an explanation for the existence of the
relative invariant in this context.