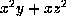 , or
, or 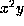 . Using the notation
introduced earlier we may assume that f is
. Using the notation
introduced earlier we may assume that f is

 If all coefficients are 0 except
If all coefficients are 0 except 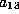 , we are done. This
means one of the other terms is not 0 and we may assume
, we are done. This
means one of the other terms is not 0 and we may assume
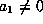 and by scaling assume
and by scaling assume 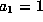 . Now set
. Now set
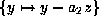 to get an equivalent form with
to get an equivalent form with 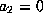 . We now
divide into two cases depending on whether or not
. We now
divide into two cases depending on whether or not 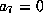 .
.