![[Shownotes]](../gif/annotate/shide-141.gif)
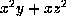 , or
, or 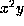 . Using the notation
introduced earlier we may assume that f is
. Using the notation
introduced earlier we may assume that f is

 If all coefficients are 0 except
If all coefficients are 0 except 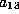 , we are done. This
means one of the other terms is not 0 and we may assume
, we are done. This
means one of the other terms is not 0 and we may assume
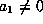 and by scaling assume
and by scaling assume 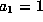 . Now set
. Now set
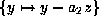 to get an equivalent form with
to get an equivalent form with 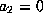 . We now
divide into two cases depending on whether or not
. We now
divide into two cases depending on whether or not 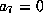 .
.
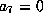 .
Now set
.
Now set 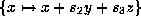 .
Let
.
Let 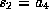 and
and 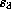 be a root of
be a root of 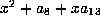 . The
resulting form has
. The
resulting form has 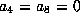 .
.
If 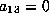 , the form is
, the form is
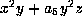 . If
. If 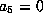 , this is
, this is 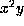 which is on the
list. Otherwise scale to get
which is on the
list. Otherwise scale to get 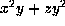 . This is
. This is
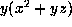 which by interchanging variables is
which by interchanging variables is 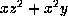 which
is on the list.
which
is on the list.
If 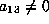 , scale to get
, scale to get 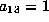 . The resulting form is
. The resulting form is
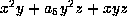 . Transforming xyz by
. Transforming xyz by
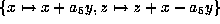 gives this form.
gives this form.
Case 2: 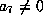 .
Scale to get
.
Scale to get 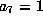 . Now transform this by
. Now transform this by
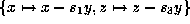 . Set
. Set 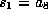 and
and 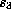 a root
of
a root
of 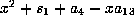 to get
to get 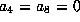 . The form is now
. The form is now
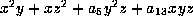 . If
. If 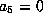 ,
this is Case 1 with the variables permuted according to
,
this is Case 1 with the variables permuted according to
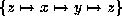 . If not it can be scaled to give
. If not it can be scaled to give
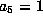 . If
. If 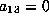 , this is
, this is 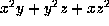 . Now
transform
. Now
transform 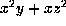 by
by 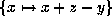 and then by
and then by
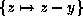 to get it.
to get it.
Assume then that 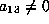 . The form is now
. The form is now
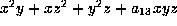 . Let a,b,c be the three distinct
roots of
. Let a,b,c be the three distinct
roots of 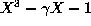 where
where 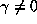 .
Now transform the form xyz by
.
Now transform the form xyz by
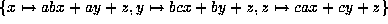 to get the form
to get the form
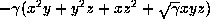 . By choosing
. By choosing
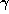 appropriately these are then all equivalent.
This transformation is found as
in by finding a linear transformation which under
conjugation transforms the Lie algebras for the centralizers of the
forms. The coeffients for the transformed xyz are obtained using
the facts that abc=1, a+b+c=0,
appropriately these are then all equivalent.
This transformation is found as
in by finding a linear transformation which under
conjugation transforms the Lie algebras for the centralizers of the
forms. The coeffients for the transformed xyz are obtained using
the facts that abc=1, a+b+c=0,
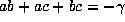 and also that
and also that
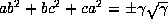 . All but the last follow
immediately because a,b,c are the roots of the equation
. All but the last follow
immediately because a,b,c are the roots of the equation
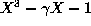 . The last follows because
. The last follows because 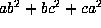 and
and 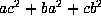 are the two roots of
are the two roots of 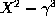 . The sum of
these terms, 0, can be found
from computing the coefficient
of
. The sum of
these terms, 0, can be found
from computing the coefficient
of 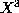 in
in 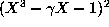 . The product,
. The product, 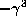 , can be evaluated
using the expressions above.
, can be evaluated
using the expressions above.