![[Shownotes]](../gif/annotate/sshow-151.gif)
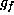 of a form f:
solvemat := proc(form,seed) local coords,modform,co,G,nullform,i,j;
coords:=[x,y,z,t];
of a form f:
solvemat := proc(form,seed) local coords,modform,co,G,nullform,i,j;
coords:=[x,y,z,t];
# map form on its projection in Z3[x,y,z,t]/Z[x^3,y^3,z^3,t^3] modform:=collect(form,coords,distributed) mod 3; for co in coords do modform:=modform-coeff(modform,co^3)*co^3 od;
# generate grad(modform,[x,y,z,t]) * G[x,y,z,t] G := linalg[matrix](4,4,subs('name'=seed,(i,j)->name.i.j)); nullform:=collect(convert([seq( diff(modform,coords[i]) * sum(G[i,j]*coords[j],j=1..4),i=1..4)],`+`),coords,distributed); for co in coords do nullform:=nullform-coeff(nullform,co^3)*co^3 od; assign(msolve(coeffs(nullform,coords),3)); G:=map(eval,G); [eval(G),indets(map(op,convert(G,listlist)))]; end:
The following algorithms are used to compute the matrix A
compmat := proc (a) local coords,x,y,z,t,M,bas_V,f,i,j,gform,co,term,c,bas,factor,k;
coords:=[x,y,z,t];
M:=array(sparse,1..16,1..16);
bas_V:=[x^2*y,x^2*z,x^2*t,y^2*x,y^2*z,y^2*t,z^2*x,z^2*y,
z^2*t,t^2*x,t^2*y,t^2*z,x*y*z,x*y*t,x*z*t,y*z*t];
f:=convert([seq(a[i]*bas_V[i],i=1..16)],`+`);
for i to 4 do
for j to 4 do
#here the OCTOBER 93 interchange of i and j occurs:
gform:=`mod`(collect(diff(f,coords[j])*coords[i],coords,distributed),3);
for co in coords do gform:=gform-coeff(gform,co^3)*co^3 od;
for term in gform do
c:=1; bas:=1;
for factor in term do
if has(factor,coords) then bas:=bas*factor else c:=c*factor fi
od;
member(bas,bas_V,'k');
M[4*i-4+j,k]:=c
od
od
od;
eval(M)
end;
The following algorithms are used to select minors from 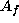 :
:
makemap := proc( remset,b1,b2 ) local res,src,trg,rem,i; if op(1,remset)<b1 or op(nops(remset),remset)>b2 then ERROR(`set contains index out of bounds`) fi; res:=array(sparse,b1..b2); src:=b1; trg:=b1; for rem in op(remset),b2+1 do for i from src to rem-1 do res[i]:=trg; trg:=trg+1 od; src:=rem+1 od; eval(res) end:
# subarray takes three parameters: a (sparse) 2-dimensional array, and two
# sets of indices. A sparse array resulting from the given one by removing
# the rows (first set) and columns (second set) specified is returned. # Remaining rows and columns will be shifted upwards and to the left.
subarray := proc( ar,rset,cset ) local bounds,r0,rn,c0,cn,rtor,ctoc,res,ind,r,c;
if not type([args],[array,set(integer),set(integer)]) then ERROR(`wrong number or type of parameters`) fi; bounds:=op(2,eval(ar)); r0:=op(1,bounds[1]); rn:=op(2,bounds[1]); c0:=op(1,bounds[2]); cn:=op(2,bounds[2]); rtor:=makemap(rset,r0,rn); ctoc:=makemap(cset,c0,cn); res:=array(sparse,r0..rn-nops(rset),c0..cn-nops(cset)); for ind in indices(ar) do r:=ind[1]; if member(",rset) then next fi; c:=ind[2]; if member(",cset) then next fi; res[rtor[r],ctoc[c]]:=ar[r,c] od; eval(res) end: