![[Shownotes]](../gif/annotate/sshow-161.gif)
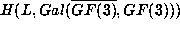 ,
for L the group of order 120 Zhijie mentions on page 25.
,
for L the group of order 120 Zhijie mentions on page 25.
In characteristic 0 we have
that 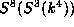 decomposes into
decomposes into 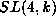 -irreducible
as follows, where the square brackets denote high weight modules
whose high weight they embrace and exponents indicate multiplicities
(bigger than one):
-irreducible
as follows, where the square brackets denote high weight modules
whose high weight they embrace and exponents indicate multiplicities
(bigger than one):

 This computation has been done using LiE, cf. [LiE].
The first factor shows that there is a form of degree 8 which is left
invariant by
This computation has been done using LiE, cf. [LiE].
The first factor shows that there is a form of degree 8 which is left
invariant by  for any field k (not necessarily of characteristic
3).
We would like to know of a geometrical explanation of this invariant
in terms of cubic surfaces in projective space.
Also, it seems reasonable to ask whether,
after modding out the invariant 4-dimensional subspace of
cubes in the case of characteristic 3, this invariant
describes the degree 8 invariant whose existence Chen derived
in [Z].
for any field k (not necessarily of characteristic
3).
We would like to know of a geometrical explanation of this invariant
in terms of cubic surfaces in projective space.
Also, it seems reasonable to ask whether,
after modding out the invariant 4-dimensional subspace of
cubes in the case of characteristic 3, this invariant
describes the degree 8 invariant whose existence Chen derived
in [Z].

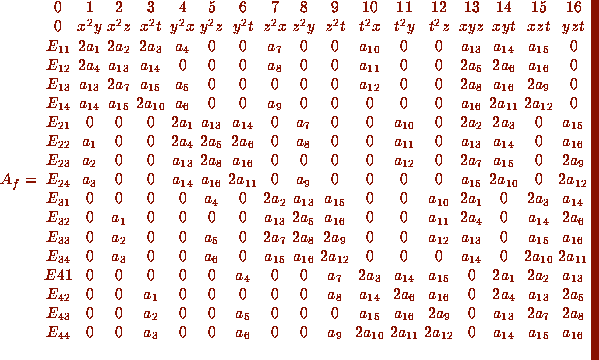
A second method we call the method of determinants. It is used when
a form is in 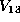 but not in
but not in 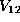 . The submatrix would be a
nonsingular
. The submatrix would be a
nonsingular 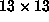 matrix so the rank of A would be 13. This
means the rows indexed by
matrix so the rank of A would be 13. This
means the rows indexed by 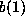 are linear combinations of the
rows of A included in the submatrix. Suppose the submatrix is
are linear combinations of the
rows of A included in the submatrix. Suppose the submatrix is
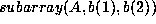 . Let
. Let 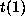 be the vector of rows not
excluded by
be the vector of rows not
excluded by 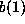 and
and 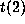 the corresponding columns of A not
excluded by
the corresponding columns of A not
excluded by 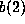 . In particular for b above,
. In particular for b above, 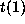 would be
would be
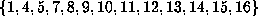 and
and 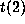 would be
would be
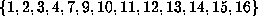 . It is straightforward to
check that the condition that A has rank 13 is
. It is straightforward to
check that the condition that A has rank 13 is

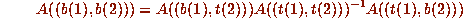 where, for
where, for 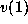 and
and 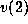 vectors, the notation
vectors, the notation 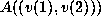 is
the submatrix of A keeping the rows in
is
the submatrix of A keeping the rows in 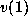 and the columns
in
and the columns
in 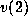 . We denote by D the
. We denote by D the 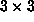 matrix above. When we
make conclusions using the method of determinants we indicate
the entry of D which gives us the information. In our cases,
the inverse can always be calculated by cofactors.
matrix above. When we
make conclusions using the method of determinants we indicate
the entry of D which gives us the information. In our cases,
the inverse can always be calculated by cofactors.