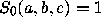When we consider Pfaff's original theorem (known today as the Pfaff-Saalschutz summation), we find that there is little to prefer in the proofs supplied by WZ and Pfaff.
The identity in question is
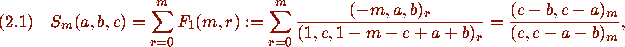where
Pfaff's proof
[11, p. 51,] (cf. [2, Section 2,]) proceeds by mathematical
induction with the initial value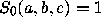 
and the recurrence
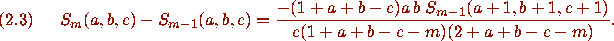
The WZ method (utilizing Zeilberger's method of creative telescoping [15]) establishes a different recurrence
Now (2.4) is a more natural recurrence than (2.3); indeed (2.4) immediately suggests the final line of (2.1), while it comes as a surprise that the final line of (2.1) satisfies (2.3).
On the other hand, (2.3) is merely term-by-term differencing of two sums while the WZ method proves (2.4) by showing that
where
is the auxiliary function called the certificate [13].
Equation (2.4) is then deduced by summing (2.5) from r=0 to
r=m+1.
Thus I would suggest that neither method is innately superior in proving (2.1).
Kummer's theorem [6, Section 2.3,] (cf. [2, Section 3,]) was the next example considered in our exposition of the Pfaff method. Again in this case, Pfaff's method and the WZ method are different but no more so than in their application to (2.1).