![[Shownotes]](../gif/annotate/shide-41.gif)
Here again the two methods diverge. The WZ method operates without a hitch as has already been shown by Zeilberger and his computer [7].
Namely, if a+f=-m and b+c+d+e=m+1, then

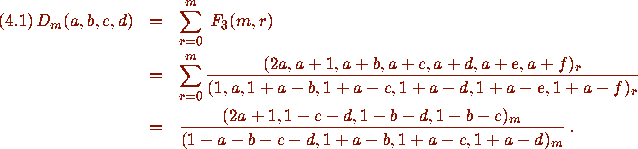
The WZ-method produces the certificate function

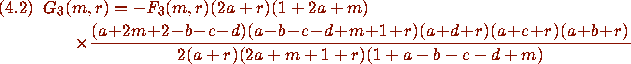 and it is then immediate that
and it is then immediate that

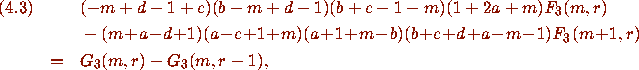 and consequently by summing (4.3) from r=0 to m+1 we find
and consequently by summing (4.3) from r=0 to m+1 we find

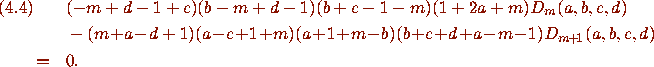
In contrast, Pfaff again is unable to prove the required result by itself. In this instance, one is forced to prove a much less known companion identity due to A. Lakin [10].
Namely if a+f=-m and b+c+d+e=m, then

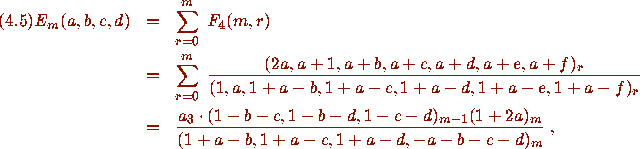 where
where 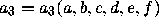 is the third elementary symmetric
function of a,b,c,d,e and f.
is the third elementary symmetric
function of a,b,c,d,e and f.
The Pfaff method now proceeds as before. In this case,

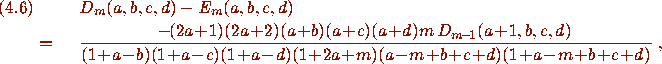 and
and

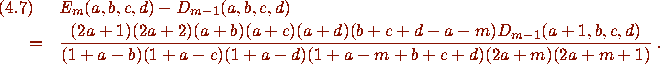 To conclude the simultaneous proof of Dougall's (4.1) and Lakin's
(4.5) theorems, one verifies that the right-hand sides satisfy (4.6)
and (4.7) also.
In this section then, the WZ method has been fast and elegant. The
Pfaff method has required the unearthing of an almost forgotten result
[10]. It has produced more but with twice the effort. If Lakin's
result had been totally forgotten, considerable computer time would
have been required to find it.
To conclude the simultaneous proof of Dougall's (4.1) and Lakin's
(4.5) theorems, one verifies that the right-hand sides satisfy (4.6)
and (4.7) also.
In this section then, the WZ method has been fast and elegant. The
Pfaff method has required the unearthing of an almost forgotten result
[10]. It has produced more but with twice the effort. If Lakin's
result had been totally forgotten, considerable computer time would
have been required to find it.
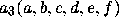 introduces. In
this instance
introduces. In
this instance

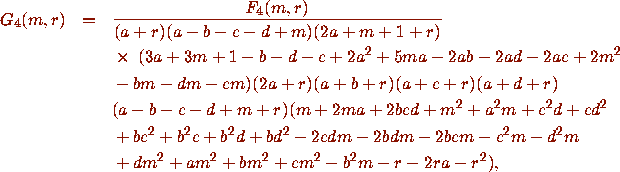 and the relevant final recurrence is
and the relevant final recurrence is

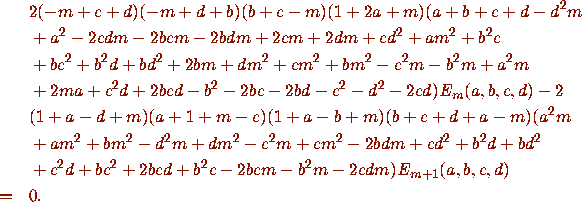
It should be pointed out here that Pfaff's method has been able to act with simpler recurrences in Sections 3 and 4 because it relies on shifts of parameters in addition to the shift of the index m.