![[Shownotes]](../gif/annotate/shide-61.gif)
Given the parallelism that we have thus far described between Pfaff
proofs and WZ-proofs, it is natural to ask if, inspired by the success
of Wilf and Petkovsek, we can find a correspondingly easier proof of
the following special case of (5.1). Let n and v be non-negative
integers with 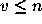 ,
,

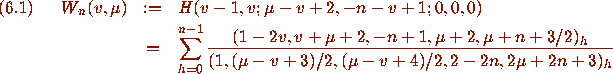 Then for v and n nonnegative integers,
Then for v and n nonnegative integers,

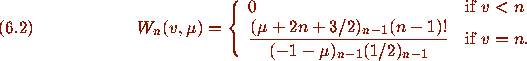 The proof of (6.2) is now quite straightforward. The bottom line
follows easily from classical summations, and the top line follows
directly from an application of Pfaff's method.
To see the bottom line we note
The proof of (6.2) is now quite straightforward. The bottom line
follows easily from classical summations, and the top line follows
directly from an application of Pfaff's method.
To see the bottom line we note

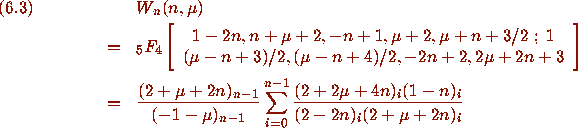 (by [6, p. 30, eq.(1),]
(Click here to see this equation)
with
(by [6, p. 30, eq.(1),]
(Click here to see this equation)
with 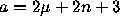 ,
, 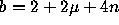 , c=1, m=n-1,
, c=1, m=n-1, 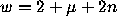 )
)

 (by [6, p. 16, Section 3.3, eq.(1),]
(Click here to see this equation)
with a = 1,
(by [6, p. 16, Section 3.3, eq.(1),]
(Click here to see this equation)
with a = 1, 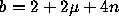 ,
, 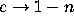 )
)
Hence the bottom line of (6.2) is proved.
For the top line of (6.2), we proceed using Pfaff's method:

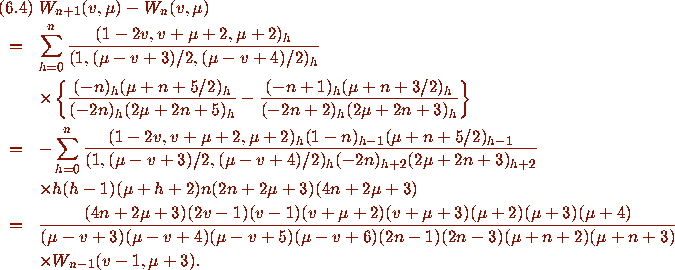
Once (6.4) is established we may set v = n and use the bottom line of (6.2) to conclude


Then by induction on i using (6.4) recursively, we conclude
that for 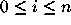 :
:

 i.e. the top line of (6.2) is valid.
i.e. the top line of (6.2) is valid.
This, then, is the result obtained by Wilf and Petkovsek and is sufficient to effect the evaluation of the Mills-Robbins-Rumsey determinant in [1].