Contents Next: References Up: Pfaff's Method (III): Comparison Previous: Rejoinder.

Conclusion.

The successive interchanges on how well the WZ method and Pfaff's method perform have made an interesting contest. Each successive discovery has added insight to our knowledge of this branch of of mathematics. I would hope that one result of this work along with that of Wilf, Petkovsek and Zeilberger is a refutation of the thesis advanced by Zeilberger in [17]. Namely, significant amounts of thought have directed computers in discovering mathematics; nowhere in all this did computers do it on their own.

I hope also that positive and constructive conclusions may be drawn from this work. Indeed, I should stress that this is not the first work to examine the limitations of the WZ method. Koorwinder [9] has a lengthy study of the WZ method and includes a discussion of some of its difficulties [9, Ex. 4.2,]. In the paper ``A Mathematica version of Zeilberger's algorithm for proving binomial coefficient identities'' by Paule and M. Schorn (to appear in the Journal of Symbolic Computation) the problem of recurrence output with non-minimal order is discussed explicitly. In sect. 4.3 one finds the example

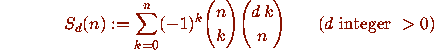for which Zeilberger's algorithm outputs a recurrence of order d - 1 instead of minimal order 1, which one expects from

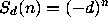. Surely, the applications of the WZ method in Section 5 (which completely surprised me) suggest that some analysis of the computational complexity of the WZ method is in order.

Also, Pfaff's method itself deserves further scrutiny. It is rare that an elegant method lies dormant for 200 years and then springs effectively to life.

In closing, I want to thank Doron Zeilberger for numerous helpful discussions and for supplying all the results described in (5.8)--(5.14).

Contents Next: References Up: Pfaff's Method (III): Comparison Previous: Rejoinder.