![[Shownotes]](../gif/annotate/sshow-91.gif)
I hope also that positive and constructive conclusions may be drawn from this work. Indeed, I should stress that this is not the first work to examine the limitations of the WZ method. Koorwinder [9] has a lengthy study of the WZ method and includes a discussion of some of its difficulties [9, Ex. 4.2,]. In the paper ``A Mathematica version of Zeilberger's algorithm for proving binomial coefficient identities'' by Paule and M. Schorn (to appear in the Journal of Symbolic Computation) the problem of recurrence output with non-minimal order is discussed explicitly. In sect. 4.3 one finds the example

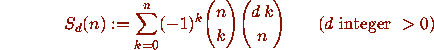 for which Zeilberger's algorithm outputs a recurrence of order
d - 1 instead of minimal order 1, which one expects from
for which Zeilberger's algorithm outputs a recurrence of order
d - 1 instead of minimal order 1, which one expects from
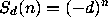 .
Surely, the applications of the WZ method in Section 5 (which
completely surprised me) suggest that some analysis of the
computational complexity of the WZ method is in order.
.
Surely, the applications of the WZ method in Section 5 (which
completely surprised me) suggest that some analysis of the
computational complexity of the WZ method is in order.
Also, Pfaff's method itself deserves further scrutiny. It is rare that an elegant method lies dormant for 200 years and then springs effectively to life.
In closing, I want to thank Doron Zeilberger for numerous helpful discussions and for supplying all the results described in (5.8)--(5.14).