![[Shownotes]](../gif/annotate/sshow-41.gif)
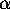 , whose value can be
computed to high precision, is algebraic of some degree n or less.
This can be done by first computing the vector
, whose value can be
computed to high precision, is algebraic of some degree n or less.
This can be done by first computing the vector 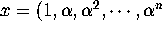 ) to high precision and then applying an
integer relation algorithm to the vector x. If a relation is found,
this integer vector is precisely the set of coefficients of a
polynomial satisfied by
) to high precision and then applying an
integer relation algorithm to the vector x. If a relation is found,
this integer vector is precisely the set of coefficients of a
polynomial satisfied by 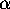 . Even if a relation is not found,
the resulting bound means that
. Even if a relation is not found,
the resulting bound means that 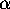 cannot possibly be the root of
a polynomial of degree n, with coefficients of size less than the
established bound. Even negative results of this sort are often of
interest.
cannot possibly be the root of
a polynomial of degree n, with coefficients of size less than the
established bound. Even negative results of this sort are often of
interest.
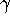 satisfies an integer polynomial of degree 50 or
less, then the Euclidean norm of the coefficients must exceed
satisfies an integer polynomial of degree 50 or
less, then the Euclidean norm of the coefficients must exceed 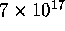 . Computations of this sort have also been applied to
study a certain conjecture regarding the Riemann zeta function. It is
well known [10] that
. Computations of this sort have also been applied to
study a certain conjecture regarding the Riemann zeta function. It is
well known [10] that

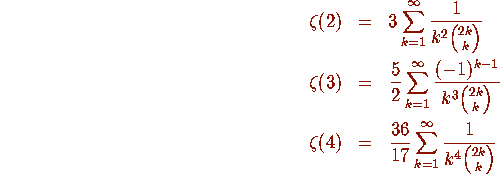 These results have led some to suggest that
These results have led some to suggest that


might also be a simple rational or algebraic number. Unfortunately,
integer relation calculations [3] have established that if
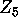 satisfies a polynomial of degree 25 or less, then the Euclidean
norm of the coefficients must exceed
satisfies a polynomial of degree 25 or less, then the Euclidean
norm of the coefficients must exceed 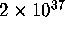 .
.
4. Euler Sums
In response to a letter from Goldbach, Euler considered sums of the form

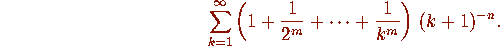
 . Little progress
has been made on this problem in the intervening years, although
special cases of Euler's results have been rediscovered numerous times
(see [7] for some references).
In April 1993, Enrico Au-Yeung, an undergraduate at the University of
Waterloo, brought to the attention of one of us the curious fact that
. Little progress
has been made on this problem in the intervening years, although
special cases of Euler's results have been rediscovered numerous times
(see [7] for some references).
In April 1993, Enrico Au-Yeung, an undergraduate at the University of
Waterloo, brought to the attention of one of us the curious fact that

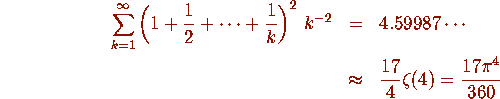
based on a computation to 500,000 terms. This author's reaction was to compute the value of this constant to a higher level of precision in order to dispel this conjecture. Surprisingly, a computation to 30 and later to 100 decimal digits still affirmed it.

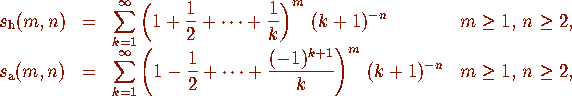
Explicit evaluations of some of the constants in these classes are
presented with proofs in [8] and [9].