![[Shownotes]](../gif/annotate/sshow-51.gif)
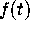 has at least 2p + 2 continuous derivatives on
has at least 2p + 2 continuous derivatives on 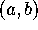 . Let D be
the differentiation operator, let
. Let D be
the differentiation operator, let 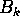 denote the k-th Bernoulli
number, and let
denote the k-th Bernoulli
number, and let 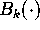 denote the k-th Bernoulli polynomial.
Then
denote the k-th Bernoulli polynomial.
Then

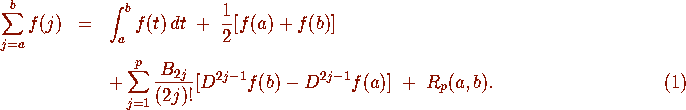 where the remainder
where the remainder 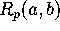 is given [2, p. 289,] by
is given [2, p. 289,] by

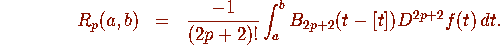
 . See
[4] for more details. Let
. See
[4] for more details. Let 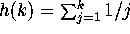 and
and
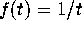 . By the Euler-Maclaurin summation formula,
. By the Euler-Maclaurin summation formula,

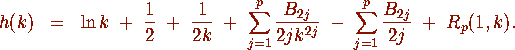 Since
Since 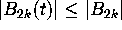 for all k and for
for all k and for 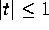 (see [1, p. 805,]), it follows that the remainder
(see [1, p. 805,]), it follows that the remainder 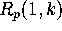 has a well-defined limit
has a well-defined limit 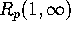 as k approaches infinity.
Now since Euler's constant
as k approaches infinity.
Now since Euler's constant 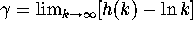 , it follows that
, it follows that

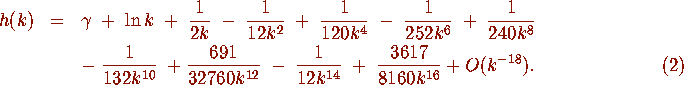 We will use
We will use 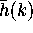 to denote this particular approximation
(i.e., (3) without the error term). Now consider the sum
to denote this particular approximation
(i.e., (3) without the error term). Now consider the sum

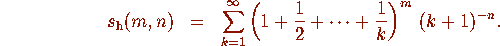
Let c be a large integer, and let 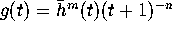 . Applying the Euler-Maclaurin summation formula (1) again,
we can write
. Applying the Euler-Maclaurin summation formula (1) again,
we can write

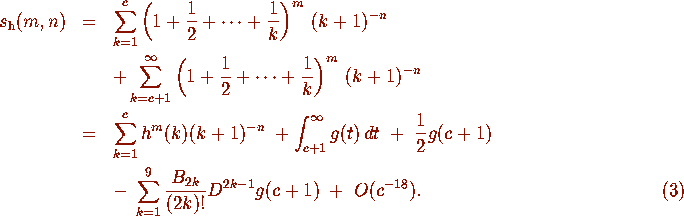
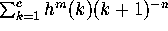 for
for 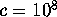 , using a numeric working precision of 150 digits. Secondly,
perform the symbolic integration and differentiation steps indicated
in formula (4). Finally, evaluate the resulting expression, again
using a working precision of 150 digits. The final result should be
equal to
, using a numeric working precision of 150 digits. Secondly,
perform the symbolic integration and differentiation steps indicated
in formula (4). Finally, evaluate the resulting expression, again
using a working precision of 150 digits. The final result should be
equal to 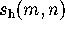 to approximately 135 significant digits.
to approximately 135 significant digits.
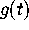 as follows: first, expand
as follows: first, expand 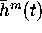 , the
numerator of
, the
numerator of 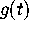 , into a sum of individual terms; next, write
, into a sum of individual terms; next, write 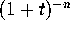 as
as 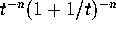 ; next, expand
; next, expand 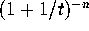 using the binomial theorem to 18 terms; next, multiply together the
resulting numerator and denominator expressions; finally, omit all
terms whose exponent of
using the binomial theorem to 18 terms; next, multiply together the
resulting numerator and denominator expressions; finally, omit all
terms whose exponent of 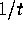 is greater than 18. The result is a
linear sum of terms of the form
is greater than 18. The result is a
linear sum of terms of the form 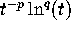 for modest-sized
integers p and q.
for modest-sized
integers p and q.
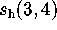 to
to 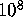 terms, using the MPFUN package with 150-digit precision arithmetic,
requires 20 hours on a ``Crimson'' workstation manufactured by Silicon
Graphics, Inc. Thus while such runs can be made, clearly this is
pressing the limits of current workstation technology. Fortunately,
it is possible to perform such computations on a highly parallel
computer system. The details of this parallel algorithm are given in
[4].
terms, using the MPFUN package with 150-digit precision arithmetic,
requires 20 hours on a ``Crimson'' workstation manufactured by Silicon
Graphics, Inc. Thus while such runs can be made, clearly this is
pressing the limits of current workstation technology. Fortunately,
it is possible to perform such computations on a highly parallel
computer system. The details of this parallel algorithm are given in
[4].