

Contents
Next: New Formulas for
Up: Recognizing Numerical
Previous: Numerical Techniques
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-61.gif)
6. Application of PSLQ to Euler Sums
The present application of Euler sum constants is well suited to
analysis with integer relation algorithms. We will present but one
example of these computations. Consider

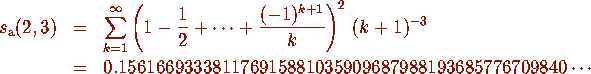 Based on experience with other constants, we conjectured that this
constant satisfies a relation involving homogeneous combinations of
Based on experience with other constants, we conjectured that this
constant satisfies a relation involving homogeneous combinations of
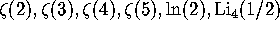 and
and
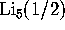 , where
, where 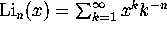 denote
s
the polylogarithm function. The numerical values of these constants,
to 50 decimal digits, are as follows:
denote
s
the polylogarithm function. The numerical values of these constants,
to 50 decimal digits, are as follows:


![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-62.gif)
The set of terms involving these constants with degree five (see
section 7) are as follows: 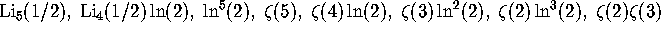 . When
. When 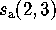 is
augmented with this set of terms, all computed to 135 decimal digits
accuracy, and the resulting 9-long vector is input to the PSLQ
algorithm, it detects the relation
is
augmented with this set of terms, all computed to 135 decimal digits
accuracy, and the resulting 9-long vector is input to the PSLQ
algorithm, it detects the relation 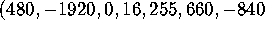 ,
, ![]() at iteration 390. Solving this relation for
at iteration 390. Solving this relation for
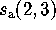 , we obtain the formula
, we obtain the formula

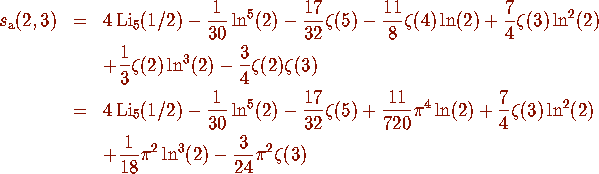 (recall that
(recall that 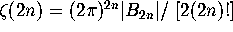 ).
When the relation is detected, the minimum and maximum y vector
entries are
).
When the relation is detected, the minimum and maximum y vector
entries are 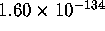 and
and 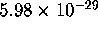 ,
respectively. Thus the confidence level of this detection is on the
order of
,
respectively. Thus the confidence level of this detection is on the
order of 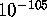 , indicating a very reliable detection.
, indicating a very reliable detection.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-63.gif)
Although 135-digit input values and 150-digit working precision were
used by us when this relation was originally detected, the fact that
the maximum y-vector entry is only 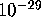 at detection implies
that such high levels of numeric precision are not required in this
case. Indeed, the above relation can be successfully detected using
only the 50-digit input values listed above and 50-digit working
precision when performing the PSLQ algorithm.
at detection implies
that such high levels of numeric precision are not required in this
case. Indeed, the above relation can be successfully detected using
only the 50-digit input values listed above and 50-digit working
precision when performing the PSLQ algorithm.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-64.gif)
Many special cases of the proven results listed in Table 1 were first
obtained using the experimental method presented in sections 2
through 4. In addition, we have obtained a number of experimental
results for which formal proofs have not yet been found. Tables 2
and 3 list some of these experimental identities. Others can be found
in [4].
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-65.gif)
It should be emphasized that the results in Tables 2 and 3 are not
established in any rigorous mathematical sense by these calculations.
However, in each case the ``confidence level'' (see section 3) of
these detections is less than 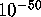 , and in most cases is in the
neighborhood of
, and in most cases is in the
neighborhood of 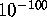 .
.

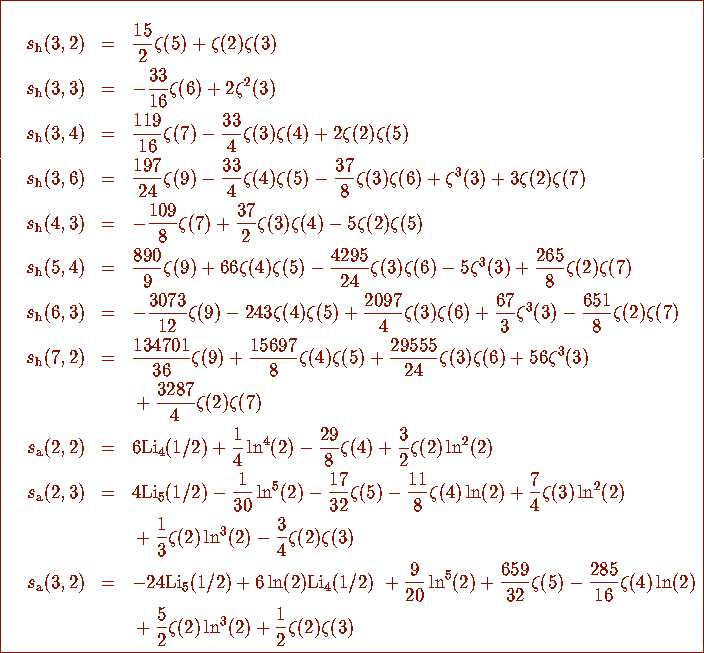
Table 1: Experimentally Detected Results
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-66.gif)
In many other cases we were not able to obtain a formula for the Euler
sum constant explicitly in terms of values of the Riemann zeta,
logarithm and polylogarithm functions, but we were able to obtain
relations involving two or more Euler sum constants of the same degree
(where by ``degree'' we mean m + n, where m and n are the
indices of the constant). Some of these relations are shown in
Table 3. This is not a complete list; we have obtained numerous other
relations of this type. The ``confidence level'' of each of these
relations is smaller than 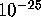 . The uniqueness of each of these
relations was checked by repeating the run with one fewer constant
input to PSLQ (there should be no relation detected when this is
done).
. The uniqueness of each of these
relations was checked by repeating the run with one fewer constant
input to PSLQ (there should be no relation detected when this is
done).


Table 2: Experimentally Detected Relations


Contents
Next: New Formulas for
Up: No Title
Previous: Numerical Techniques
![[Shownotes]](../gif/annotate/sshow-61.gif)

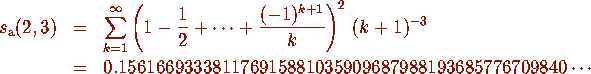 Based on experience with other constants, we conjectured that this
constant satisfies a relation involving homogeneous combinations of
Based on experience with other constants, we conjectured that this
constant satisfies a relation involving homogeneous combinations of
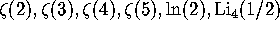 and
and
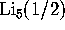 , where
, where 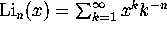 denote
s
the polylogarithm function. The numerical values of these constants,
to 50 decimal digits, are as follows:
denote
s
the polylogarithm function. The numerical values of these constants,
to 50 decimal digits, are as follows:


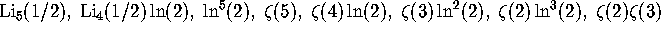 . When
. When 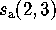 is
augmented with this set of terms, all computed to 135 decimal digits
accuracy, and the resulting 9-long vector is input to the PSLQ
algorithm, it detects the relation
is
augmented with this set of terms, all computed to 135 decimal digits
accuracy, and the resulting 9-long vector is input to the PSLQ
algorithm, it detects the relation 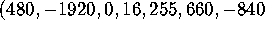 ,
, 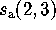 , we obtain the formula
, we obtain the formula

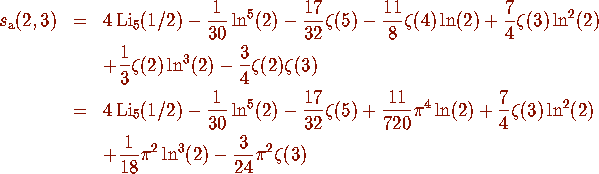 (recall that
(recall that 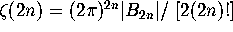 ).
When the relation is detected, the minimum and maximum y vector
entries are
).
When the relation is detected, the minimum and maximum y vector
entries are 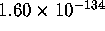 and
and 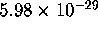 ,
respectively. Thus the confidence level of this detection is on the
order of
,
respectively. Thus the confidence level of this detection is on the
order of 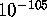 , indicating a very reliable detection.
, indicating a very reliable detection.
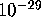 at detection implies
that such high levels of numeric precision are not required in this
case. Indeed, the above relation can be successfully detected using
only the 50-digit input values listed above and 50-digit working
precision when performing the PSLQ algorithm.
at detection implies
that such high levels of numeric precision are not required in this
case. Indeed, the above relation can be successfully detected using
only the 50-digit input values listed above and 50-digit working
precision when performing the PSLQ algorithm.
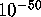 , and in most cases is in the
neighborhood of
, and in most cases is in the
neighborhood of 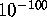 .
.

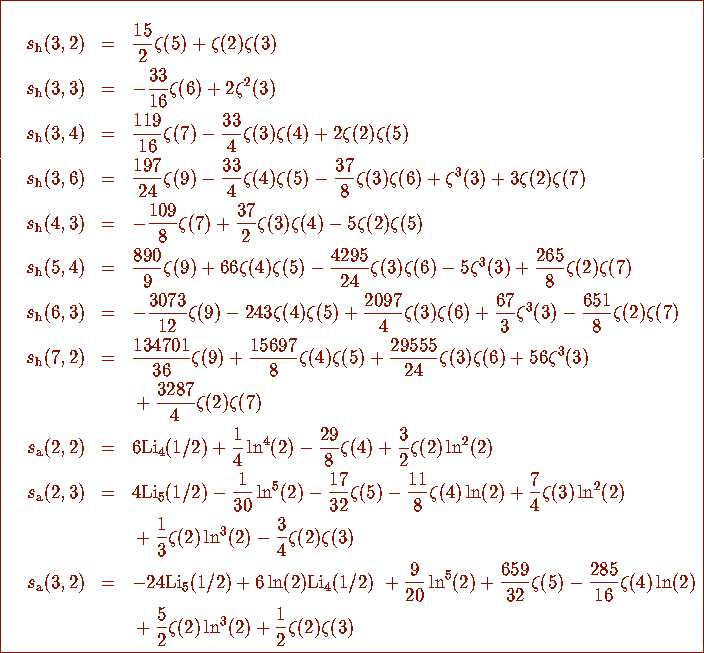
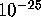 . The uniqueness of each of these
relations was checked by repeating the run with one fewer constant
input to PSLQ (there should be no relation detected when this is
done).
. The uniqueness of each of these
relations was checked by repeating the run with one fewer constant
input to PSLQ (there should be no relation detected when this is
done).

