One of the interesting morals from theoretical computer
science is that many familiar algorithms are far from optimal. In order to be more
precise we introduce the notion of bit complexity. Bit complexity counts the
number of single operations required to complete an algorithm. The single-digit
operations are +, -, 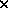 . (We could, if we wished, introduce storage and
logical comparison into the count. This, however, doesn't affect the order of growth
of the algorithms in which we are interested.) This is a good measure of time on a
serial machine. Thus, addition of two n-digit integers by the usual method has bit
complexity
. (We could, if we wished, introduce storage and
logical comparison into the count. This, however, doesn't affect the order of growth
of the algorithms in which we are interested.) This is a good measure of time on a
serial machine. Thus, addition of two n-digit integers by the usual method has bit
complexity 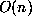 , straightforward uniqueness considerations show this to be
asymptotically best possible.
, straightforward uniqueness considerations show this to be
asymptotically best possible.
 Annotation Form Interface
Annotation Form Interface
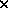 . (We could, if we wished, introduce storage and
logical comparison into the count. This, however, doesn't affect the order of growth
of the algorithms in which we are interested.) This is a good measure of time on a
serial machine. Thus, addition of two n-digit integers by the usual method has bit
complexity
. (We could, if we wished, introduce storage and
logical comparison into the count. This, however, doesn't affect the order of growth
of the algorithms in which we are interested.) This is a good measure of time on a
serial machine. Thus, addition of two n-digit integers by the usual method has bit
complexity 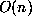 , straightforward uniqueness considerations show this to be
asymptotically best possible.
, straightforward uniqueness considerations show this to be
asymptotically best possible.