![[Shownotes]](../gif/annotate/shide-111.gif)
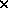 . (We could, if we wished, introduce storage and
logical comparison into the count. This, however, doesn't affect the order of growth
of the algorithms in which we are interested.) This is a good measure of time on a
serial machine. Thus, addition of two n-digit integers by the usual method has bit
complexity
. (We could, if we wished, introduce storage and
logical comparison into the count. This, however, doesn't affect the order of growth
of the algorithms in which we are interested.) This is a good measure of time on a
serial machine. Thus, addition of two n-digit integers by the usual method has bit
complexity 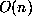 , straightforward uniqueness considerations show this to be
asymptotically best possible.
, straightforward uniqueness considerations show this to be
asymptotically best possible.
Multiplication is a different story. Usual multiplication of two n-digit integers
has bit complexity 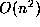 and no better. However, it is possible to multiply two
n-digit integers with complexity
and no better. However, it is possible to multiply two
n-digit integers with complexity 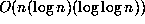 . This result is due to
Schönhage and Strassen and dates from 1971 [29]. It provides the best
bound known for multiplication. No multiplication can have speed better than
. This result is due to
Schönhage and Strassen and dates from 1971 [29]. It provides the best
bound known for multiplication. No multiplication can have speed better than
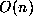 . Unhappily, more exact results aren't available.
. Unhappily, more exact results aren't available.
The original observation that a faster than 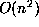 multiplication is possible was due
to Karatsuba in 1962. Observe that
multiplication is possible was due
to Karatsuba in 1962. Observe that

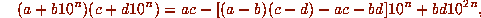 and thus multiplication of two 2n-digit integers can be reduced to three
multiplications of n-digit integers and a few extra additions. (Of course
multiplication by
and thus multiplication of two 2n-digit integers can be reduced to three
multiplications of n-digit integers and a few extra additions. (Of course
multiplication by 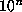 is just a shift of the decimal point.) If one now proceeds
recursively one produces a multiplication with bit complexity
is just a shift of the decimal point.) If one now proceeds
recursively one produces a multiplication with bit complexity

 Note that
Note that 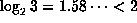 .
We denote by
.
We denote by 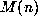 the bit complexity of multiplying two n-digit integers together
by any method that is at least as fast as usual multiplication.
the bit complexity of multiplying two n-digit integers together
by any method that is at least as fast as usual multiplication.
The trick to implementing high precision arithmetic is to get the multiplication right. Division and root extraction piggyback off multiplication using Newton's method. One may use the iteration

 to compute
to compute 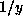 and the iteration
and the iteration

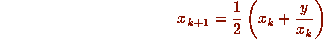 to compute
to compute 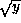 . One may also compute
. One may also compute 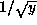 from
from

 and so avoid divisions in the computation of
and so avoid divisions in the computation of 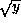 . Not only do these
iterations converge quadratically but, because Newton's method is self-correcting (a
slight perturbation in
. Not only do these
iterations converge quadratically but, because Newton's method is self-correcting (a
slight perturbation in 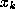 does not change the limit), it is possible at the kth
stage to work only to precision
does not change the limit), it is possible at the kth
stage to work only to precision 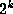 . If division and root extraction are so
implemented, they both have bit complexity
. If division and root extraction are so
implemented, they both have bit complexity 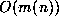 , in the sense that n-digit
input produces n-digit accuracy in a time bounded by a constant times the speed of
multiplication. This extends in the obvious way to the solution of any algebraic
equation, with the startling conclusion that every algebraic number can be computed
(to n-digit accuracy) with bit complexity
, in the sense that n-digit
input produces n-digit accuracy in a time bounded by a constant times the speed of
multiplication. This extends in the obvious way to the solution of any algebraic
equation, with the startling conclusion that every algebraic number can be computed
(to n-digit accuracy) with bit complexity 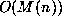 . Writing down n digits of
. Writing down n digits of
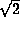 or
or 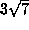 is (up to a constant) no more complicated than
multiplication.
The Schönhage-Strassen multiplication is hard to implement. However, a
multiplication with complexity
is (up to a constant) no more complicated than
multiplication.
The Schönhage-Strassen multiplication is hard to implement. However, a
multiplication with complexity 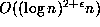 based on an ordinary
complex (floating point) fast Fourier transform is reasonably straightforward. This
is Kanada's approach, and the recent records all rely critically on some variations
of this technique.
based on an ordinary
complex (floating point) fast Fourier transform is reasonably straightforward. This
is Kanada's approach, and the recent records all rely critically on some variations
of this technique.
To see how the fast Fourier transform may be used to accelerate multiplication, let
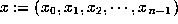 and
and 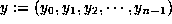 be the representations of two high-precision numbers in some radix b. The radix
b is usually selected to be some power of 2 or 10 whose square is less than the
largest integer exactly representable as an ordinary floating-point number on the
computer being used. Then, except for releasing each ``carry'', the product
be the representations of two high-precision numbers in some radix b. The radix
b is usually selected to be some power of 2 or 10 whose square is less than the
largest integer exactly representable as an ordinary floating-point number on the
computer being used. Then, except for releasing each ``carry'', the product 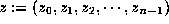 of x and y may be written as
of x and y may be written as

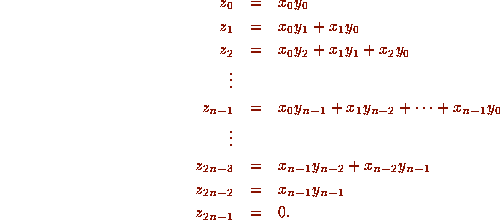 Now consider x and y to have n zeros appended, so that x, y, and z all
have length N =2n. Then a key observation may be made: the product sequence z is
precisely the discrete convolution
Now consider x and y to have n zeros appended, so that x, y, and z all
have length N =2n. Then a key observation may be made: the product sequence z is
precisely the discrete convolution  :
:

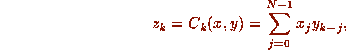 where the subscript k-j is to be interpreted as k-j +N if k-j is negative.
where the subscript k-j is to be interpreted as k-j +N if k-j is negative.
Now a well-known result of Fourier analysis may be applied. Let 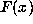 denote the
discrete Fourier transform of the sequence x, and let
denote the
discrete Fourier transform of the sequence x, and let 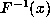 denote the
inverse discrete Fourier transform of x:
denote the
inverse discrete Fourier transform of x:

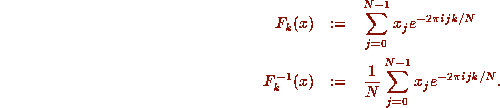 Then the ``convolution theorem'', whose proof is a straightforward exercise, states
that
Then the ``convolution theorem'', whose proof is a straightforward exercise, states
that

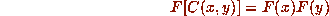 or, expressed another way,
or, expressed another way,

 Thus the entire multiplication pyramid z can be obtained by performing two forward
discrete Fourier transforms, one vector complex multiplication and one inverse
transform, each of length N =2n. Once the real parts of the resulting complex
numbers have been rounded to the nearest integer, the final mutiprecision product
may be obtained by merely releasing the carries modulo b. This may be done by
starting at the end of the z vector and working backward, as in elementary school
arithmetic, or by applying other schemes suitable for vector processing on more
sophisticated computers.
Thus the entire multiplication pyramid z can be obtained by performing two forward
discrete Fourier transforms, one vector complex multiplication and one inverse
transform, each of length N =2n. Once the real parts of the resulting complex
numbers have been rounded to the nearest integer, the final mutiprecision product
may be obtained by merely releasing the carries modulo b. This may be done by
starting at the end of the z vector and working backward, as in elementary school
arithmetic, or by applying other schemes suitable for vector processing on more
sophisticated computers.
A straightforward implementation of the above procedure would not result in any
computational savings --- in fact, it would be several times more costly than the
usual ``schoolperson'' scheme. The reason this scheme is used is that the discrete
Fourier transform may be computed much more rapidly using some variation of the
well-known ``fast Fourier transform'' (FFT) algorithm [13]. In particular,
if 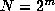 , then the discrete Fourier transform may be evaluated in only
, then the discrete Fourier transform may be evaluated in only 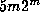 arithmetic operations using an FFT. Direct application of the definition of the
discrete Fourier transform would require
arithmetic operations using an FFT. Direct application of the definition of the
discrete Fourier transform would require 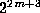 floating-point arithmetic
operations, even if it is assumed that all powers of
floating-point arithmetic
operations, even if it is assumed that all powers of 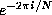 have been
precalculated.
have been
precalculated.
This is the basic scheme for high-speed multiprecision multiplication. Many details
of efficient implementations have been omitted. For example, it is possible to take
advantage of the fact that the input sequences x and y and the output sequence z
are all purely real numbers, and thereby sharply reduce the operation count. Also, it
is possible to dispense with complex numbers altogether in favor of performing
computations in fields of integers modulo large prime numbers. Interested readers
are referred to [2], [8], [13], and [22].
When the costs of all the constituent operations, using the best known techniques,
are totalled both Algorithms 1 and 2 compute n digits of  with bit complexity
with bit complexity
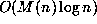 , and use
, and use 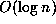 full precision operations.
full precision operations.
The bit complexity for Sum 1, or for  using any of the arctan expansions, is
between
using any of the arctan expansions, is
between 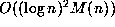 and
and 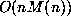 depending on implementation. In each
case, one is required to sum
depending on implementation. In each
case, one is required to sum 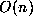 terms of the appropriate series. Done naively,
one obtains the latter bound. If the calculation is carefully orchestrated so that
the terms are grouped to grow evenly in size (as rational numbers) then one can
achieve the former bound, but with no corresponding reduction in the number of
operations.
The Archimedean iteration of section 2 converges like
terms of the appropriate series. Done naively,
one obtains the latter bound. If the calculation is carefully orchestrated so that
the terms are grouped to grow evenly in size (as rational numbers) then one can
achieve the former bound, but with no corresponding reduction in the number of
operations.
The Archimedean iteration of section 2 converges like 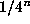 so in excess of n
iterations are needed for n-digit accuracy, and the bit complexity is
so in excess of n
iterations are needed for n-digit accuracy, and the bit complexity is 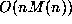 .
.
Almost any familiar transcendental number such as e, 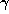 ,
, 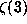 , or
Catalan's constant (presuming the last three to be nonalgebraic) can be computed
with bit complexity
, or
Catalan's constant (presuming the last three to be nonalgebraic) can be computed
with bit complexity 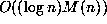 or
or 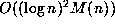 . None of these numbers
is known to be computable essentially any faster than this. In light of the
previous observation that algebraic numbers are all computable with bit complexity
. None of these numbers
is known to be computable essentially any faster than this. In light of the
previous observation that algebraic numbers are all computable with bit complexity
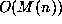 , a proof that
, a proof that  cannot be computed with this speed would imply the
transcendence of
cannot be computed with this speed would imply the
transcendence of  . It would, in fact, imply more, as there are transcendental
numbers which have complexity
. It would, in fact, imply more, as there are transcendental
numbers which have complexity 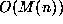 . An example is
. An example is 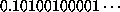 .
It is also reasonable to speculate that computing the nth digit of
.
It is also reasonable to speculate that computing the nth digit of  is not
very much easier than computing all the first n digits. We think it very probable
that computing the nth digit of
is not
very much easier than computing all the first n digits. We think it very probable
that computing the nth digit of  cannot be
cannot be 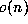 .
.