![[Shownotes]](../gif/annotate/sshow-101.gif)
Bailey in January 1986 computed over 29 million digits using Algorithm 1 on a Cray 2
[2]. Kanada [33], using a related quadratic algorithm (due in basis to Gauss
and made explicit by Brent [12] and Salamin [25] [27]) and using
Algorithm 1 for a check, verified 33,554,000 digits. This employed a HITACHI
S--810/20, took roughly eight hours and was completed in September of 1986. In
January 1987 Kanada extended his computation to 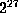 decimal places of
decimal places of  and
the hundred million digit mark had been passed. The calculation took roughly a day
and a half on a NEC SX2 machine. Kanada's most recent feat (Jan. 1988) was to compute
201,326,000 digits, which required only six hours on a new Hitachi S-820
supercomputer.
Within the next few years
many
hundreds of millions
of digits will no
doubt have been similarly computed. Further discussion of the history of the
computation of
and
the hundred million digit mark had been passed. The calculation took roughly a day
and a half on a NEC SX2 machine. Kanada's most recent feat (Jan. 1988) was to compute
201,326,000 digits, which required only six hours on a new Hitachi S-820
supercomputer.
Within the next few years
many
hundreds of millions
of digits will no
doubt have been similarly computed. Further discussion of the history of the
computation of  may be found in [5] and [9].
may be found in [5] and [9].