![[Shownotes]](../gif/annotate/sshow-91.gif)

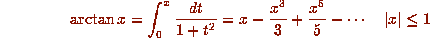 coupled with a formula which allows small x to be used, like
coupled with a formula which allows small x to be used, like

 This particular formula is due to
Machin
and was employed by him to compute 100
digits of
This particular formula is due to
Machin
and was employed by him to compute 100
digits of  in 1706. Variations on this second theme are the basis of all the
calculations done until the 1970's including William
Shanks'
monumental
hand-calculation of 527 digits. In the introduction to his book [32],
which presents this calculation, Shanks writes:
in 1706. Variations on this second theme are the basis of all the
calculations done until the 1970's including William
Shanks'
monumental
hand-calculation of 527 digits. In the introduction to his book [32],
which presents this calculation, Shanks writes:
Towards the close of the year 1850 the Author first formed the design of rectifying the circle upwards of 300 places of decimals. He was fully aware at that time, that the accomplishment of his purpose would add little or nothing to his fame as a Mathematician though it might as a Computer: nor would it be productive of anything in the shape of pecuniary recompense.
Shanks actually attempted to hand-calculate 707 digits but a mistake crept in at the 527th digit. This went unnoticed until 1945, when D. Ferguson, in one of the last ``nondigital'' calculations, computed 530 digits. Even with machine calculations mistakes occur, so most record-setting calculations are done twice --- by sufficiently different methods.
The advent of computers has greatly increased the scope and decreased the toil of such
calculations. Metropolis, Reitwieser, and von Neumann computed and analyzed 2037
digits using Machin's formula on ENIAC in 1949. In 1961, Dan Shanks and Wrench
calculated 100,000 digits on an IBM 7090 [31]. By 1973, still using
Machin-like arctan expansions, the million digit mark was passed by Guilloud and
Bouyer on a CDC 7600.