![[Shownotes]](../gif/annotate/sshow-11.gif)
Gregory's series
for 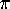 , truncated at 500,000 terms gives to forty places
, truncated at 500,000 terms gives to forty places




Only the underlined digits are wrong. This is explained by the following Theorem.

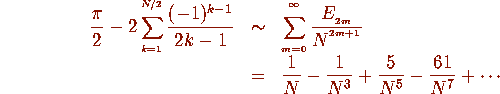 where the coefficients are
the even Euler numbers 1, -1, 5, -61, 1385,
where the coefficients are
the even Euler numbers 1, -1, 5, -61, 1385,
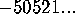 .
.
Gregory's series requires more terms than there are particles
in the universe to compute 100 digits of 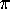 .
.
However, with N = 200,000 and correcting using
the first thousand even Euler numbers gives over 5,000 digits of 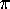 .
.
See Pi, Euler numbers and asymptotic expansions by J. Borwein, P. Borwein & K. Dilcher in the MAA Monthly 96 (1989) 681-687.

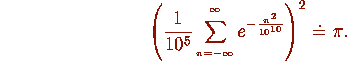
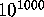 th digit of
th digit of
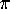 (or the
(or the 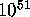 th).
th).