![[Shownotes]](../gif/annotate/sshow-51.gif)
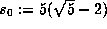 and
and 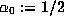 .
Let
.
Let

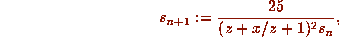 where
where

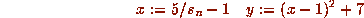 and
and

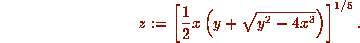 Let
Let

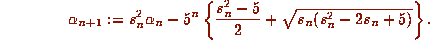 Then
Then

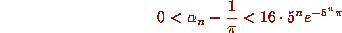 and
and 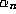 converges to
converges to 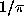 quintically (that is, with order five).
quintically (that is, with order five).
Each additional term in Sum 1 adds roughly eight digits, each additional iteration of
Algorithm 1 quadruples the number of correct digits, while each additional iteration
of Algorithm 2 quintuples the number of correct digits. Thus a mere thirteen
iterations of Algorithm 2 provide in excess of one billion decimal digits of  . In
general, for us, pth-order convergence of a sequence
. In
general, for us, pth-order convergence of a sequence 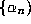 to
to  means that
means that 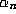 tends to
tends to  and that
and that

 for some constant C >0. Algorithm 1 is
arguably the most efficient algorithm
currently known for the extended precision calculation of
for some constant C >0. Algorithm 1 is
arguably the most efficient algorithm
currently known for the extended precision calculation of  . While the rates of
convergence are impressive, it is the subtle and thoroughly nontransparent nature of
these results and the beauty of the underlying mathematics that intrigue us most.
. While the rates of
convergence are impressive, it is the subtle and thoroughly nontransparent nature of
these results and the beauty of the underlying mathematics that intrigue us most.
Watson[37], commenting on certain formulae of Ramanujan, talks of
a thrill which is indistinguishable from the thrill which I feel when I enter the Sagrestia Nuovo of the Capella Medici and see before me the austere beauty of the four statues representing ``Day'', ``Night'', ``Evening'', and ``Dawn'' which Michelangelo has set over the tomb of Giuliano de'Medici and Lorenzo de'Medici.
Sum 1 is directly due to Ramanujan and appears in [26]. It rests on a
modular identity of order 58 and, like much of Ramanujan's work, appears without proof
and with only scanty motivation. The first derivation we know of appears in
[11]. Algorithms 1 and 2 are based on modular identities of orders 4 and
5 respectively. The underlying quintic modular identity in Algorithm 2 (the relation
for 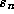 ) is also due to Ramanujan, though the first proof is due to Berndt and
appears in [7].
) is also due to Ramanujan, though the first proof is due to Berndt and
appears in [7].
One intention in writing this article is to explain the genesis of Sum 1 and of Algorithms 1 and 2. It is not possible to give a short self-contained account without assuming an unusual degree of familiarity with modular function theory. Also, parts of the derivation involve considerable algebraic calculation and may most easily be done with the aid of a symbolic manipulation package (MACSYMA, MAPLE, REDUCE, etc.) . We hope however to give a taste of methods involved. The full details are available in [11].
A second intention is very briefly to describe the role of these and related
approximations in the recent extended precision calculations of  . In part this
entails a short discussion of the complexity and implementation of such calculations.
This centers on a discussion of multiplication by fast Fourier transform methods. Of
considerable related interest is the fact that these algorithms for
. In part this
entails a short discussion of the complexity and implementation of such calculations.
This centers on a discussion of multiplication by fast Fourier transform methods. Of
considerable related interest is the fact that these algorithms for  are provably
close to the theoretical optimum.
are provably
close to the theoretical optimum.