![[Shownotes]](../gif/annotate/sshow-61.gif)
 is almost certainly the most
natural
of the transcendental numbers, arising as the circumference of a circle of
unit diameter. Thus, it is not surprising that its properties have been studied for
some twenty-five hundred years. What is surprising is how little we actually know.
is almost certainly the most
natural
of the transcendental numbers, arising as the circumference of a circle of
unit diameter. Thus, it is not surprising that its properties have been studied for
some twenty-five hundred years. What is surprising is how little we actually know.
We know that  is irrational, and have known this since
Lambert's
proof of 1771
(see [5]). We have known that
is irrational, and have known this since
Lambert's
proof of 1771
(see [5]). We have known that  is
transcendental
since
Lindemann's
proof of 1882 [23]. We also know that
is
transcendental
since
Lindemann's
proof of 1882 [23]. We also know that  is not a Liouville number.
Mahler proved this in 1953. An irrational number
is not a Liouville number.
Mahler proved this in 1953. An irrational number 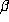 is Liouville if, for
any n, there exist integers p and q so that
is Liouville if, for
any n, there exist integers p and q so that

 Liouville showed these numbers are all transcendental. In fact we know that
Liouville showed these numbers are all transcendental. In fact we know that

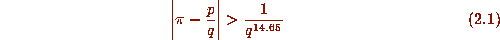 for p,q integral with q sufficiently large. This irrationality estimate,
due to Chudnovsky and Chudnovsky [16] is certainly
not the best possible
. It is likely that 14.65 should be replaced by
for p,q integral with q sufficiently large. This irrationality estimate,
due to Chudnovsky and Chudnovsky [16] is certainly
not the best possible
. It is likely that 14.65 should be replaced by 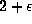 for any
for any 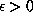 .
Almost all transcendental numbers satisfy such an inequality. We know a few related
results for the rate of algebraic approximation. The results may be pursued in
[4] and [11].
.
Almost all transcendental numbers satisfy such an inequality. We know a few related
results for the rate of algebraic approximation. The results may be pursued in
[4] and [11].
We know that 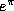 is transcendental. This follows by noting that
is transcendental. This follows by noting that 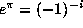 and applying the Gelfond-Schneider theorem [4]. We know that
and applying the Gelfond-Schneider theorem [4]. We know that 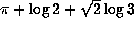 is transcendental. This result is a consequence of the work
that won Baker a Fields Medal in 1970. And we know a few more than the first two
hundred million digits of the decimal expansion for
is transcendental. This result is a consequence of the work
that won Baker a Fields Medal in 1970. And we know a few more than the first two
hundred million digits of the decimal expansion for  (Kanada, see Section 3).
(Kanada, see Section 3).
The state of our ignorance is more profound. We do not know whether such basic
constants as 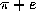 ,
, 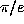 or
or 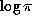 are irrational, let alone
transcendental. The best we can say about these three particular constants is that
they cannot satisfy any polynomial of degree eight or less with integer coefficients
of average size less than
are irrational, let alone
transcendental. The best we can say about these three particular constants is that
they cannot satisfy any polynomial of degree eight or less with integer coefficients
of average size less than 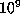 [3]. This is a consequence of some recent
computations employing the Ferguson-Forcade algorithm [17]. We don't know
anything of consequence about the simple continued fraction of
[3]. This is a consequence of some recent
computations employing the Ferguson-Forcade algorithm [17]. We don't know
anything of consequence about the simple continued fraction of  , except
(numerically) the first 17 million terms, which Gosper computed in 1985 using Sum 1.
Likewise, apart from listing the first many millions of digits of
, except
(numerically) the first 17 million terms, which Gosper computed in 1985 using Sum 1.
Likewise, apart from listing the first many millions of digits of  , we know
virtually nothing about the decimal expansion of
, we know
virtually nothing about the decimal expansion of  . It is possible, albeit not a
good bet, that all but finitely many of the decimal digits of
. It is possible, albeit not a
good bet, that all but finitely many of the decimal digits of  are in fact 0's
and 1's. Carl Sagan's recent novel Contact rests on a similar possibility.
Questions concerning the normality of or the distribution of digits of particular
transcendentals such as
are in fact 0's
and 1's. Carl Sagan's recent novel Contact rests on a similar possibility.
Questions concerning the normality of or the distribution of digits of particular
transcendentals such as  appear completely beyond the scope of current
mathematical techniques. The evidence from analysis of the first thirty million
digits is that they are very uniformly distributed [2]. The next one
hundred and seventy million digits apparently contain no surprises.
appear completely beyond the scope of current
mathematical techniques. The evidence from analysis of the first thirty million
digits is that they are very uniformly distributed [2]. The next one
hundred and seventy million digits apparently contain no surprises.
In part we perhaps settle for computing digits of  because there
is little else
we can currently do. We would be amiss, however, if we did not emphasize that the
extended precision calculation of
because there
is little else
we can currently do. We would be amiss, however, if we did not emphasize that the
extended precision calculation of  has substantial application as a test of the
``global integrity'' of a supercomputer. The extended precision calculations
described in Section 3 uncovered hardware errors which had to be corrected before
those calculations could successfully run. Such calculations, implemented as in
Section 4, are apparently now used routinely to check supercomputers before they leave
the factory. A large-scale calculation of
has substantial application as a test of the
``global integrity'' of a supercomputer. The extended precision calculations
described in Section 3 uncovered hardware errors which had to be corrected before
those calculations could successfully run. Such calculations, implemented as in
Section 4, are apparently now used routinely to check supercomputers before they leave
the factory. A large-scale calculation of  is entirely
unforgiving
; it soaks into
all parts of the machine and a single bit awry leaves detectable consequences.
is entirely
unforgiving
; it soaks into
all parts of the machine and a single bit awry leaves detectable consequences.